Goniometricka funkce
Dobrý den.
Potřeboval bych od někoho ochotného, jestli by mohl mi nějak názorně a s náčrtkem a řešením krok po kroku vypočítat 2 příklady na goniometrickou funkci. Moc jsem tomu neporozuměl, tak bych potřeboval vidět ten postup, abych další zvládnul už zas sám.
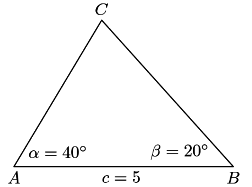
Řešte trojúhelník ABC, je li dáno c = 5cm, alfa = 40°, beta = 20°
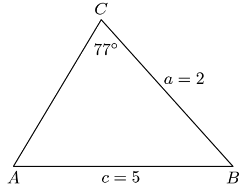
Řešte trojúhelník ABC, je li dáno a = 2cm, c = 5cm, gama = 77°
Jan B.
29. 03. 2021 07:47
3 odpovědi
Ahoj,
v 1. úloze nejdříve dopočítáme úhel \( \gamma=120^{ \circ} \). Dále použijeme sinovou větu, kterou při řešení úloh obvykle zapisujeme ve tvaru
\(\frac{ a} { b} =\frac{ \sin\alpha} { \sin\beta} ,\quad \frac{ b} { c} =\frac{ \sin\beta} { \sin\gamma} ,\quad \frac{ c} { a} =\frac{ \sin\gamma} { \sin\alpha} \)
a podobně.
Známe stranu \( c \), vypočítáme nejdříve třeba stranu \( a \), sinovou větu zapíšeme
\(\frac{ a} { c} =\frac{ \sin\alpha} { \sin\gamma} \)
odtud
\(a=\frac{ c\cdot \sin\alpha} { \sin\gamma} \)
\(a=\frac{ 5\cdot \sin 40^{ \circ} } { \sin 120^{ \circ} } =\frac{ 5\cdot 0.6428} { 0.8660} =3.71\phantom{ .} { \rm cm} \).
Pro výpočet strany \( b \) zapíšeme sinovou větu
\(\frac{ b} { c} =\frac{ \sin\beta} { \sin\gamma} \)
a postupujeme obdobně, vyjde \( b=1.97 \phantom{ .} { \rm cm} \).
Ve 2. úloze vypočítáme třeba nejprve úhel \( \alpha \). Podle sinové věty (výhodně zaměníme strany, abychom měli sinus nalevo)
\(\frac{ \sin\alpha} { \sin\gamma} =\frac{ a} { c} \)
odtud
\( \sin\alpha=\frac{ a} { c} \cdot \sin\gamma \)
dosadíme
\( \sin\alpha=\frac{ 2} { 5} \cdot \sin 77^o=\frac{ 2} { 5} \cdot 0.9744=0.3897\)
hledáme úhel alfa, pro který platí
\( \sin\alpha=0.3897\)
Rovnice má v intervalu \( (0^o, 180^o) \) dvě řešení: \( \alpha_1=22^o 56', \alpha_2=157^o 04' \). Druhé řešení nevyhovuje, protože \( \alpha_2+\gamma >180^o \). Je tedy \( \alpha=22^o 56' \).
Dopočítáme úhel \( \beta=180-(\gamma+\alpha)=80^o 04' \).
Dále vypočítáme např. stranu \( b \):
\(\frac{ b} { c} =\frac{ \sin\beta} { \sin\gamma} \)
odtud
\(b=\frac{ c\cdot\sin\beta} { \sin\gamma} \)
dosadíme
\(b=\frac{ 5\cdot\sin80^o 04'} { \sin77^o} =\frac{ 5\cdot0.9850} { 0.9744} =5.05\phantom{ .} { \rm cm} \).
Mockrát děkuju, už se v tom orientuju trochu víc. Fakt díky!