Goniometrické funkce
Hezký den.
Pomůže mi někdo s řešením tohoto příkladu.
Z bodu na kružnici o průměru 8 cm jsou vedeny dvě shodné tětivy, které svírají úhel 60°.Vypočítej délku tětiv.
Tento příklad lze vyřešit pomocí cosinové věty (ovšem to je látka ze střední školy).Tento příklad byl zadán v rámci příprav na přijímačky na střední školy.
Nevím, zdali tento příklad má vůbec nějaké řešení v rámci probíraného učiva na základní škole. Předem děkuji za odpověd.
Tadeáš M.
22. 06. 2020 13:18
13 odpovědí
Na přijímačky goniometricke funkce být nemůžou.
Nikdy nebyly, a pochybuji že by byly.
To já souhlasím. Chtěl bych jenom vědět, zda tento příklad jde nějakým způsobem spočítat a nepoužít cosinové věty (třeba i pomocí matematických tabulek) a použít při řešení pouze učivo ze základní školy.....
Cos by jse měl na základce objevit v 9 třídě i sin, tan.
Ale jenom někteří učitele to dělají, protože se to na SŠ teprve pořádně probere. Příklady v matematice mají obrovský počet řešení, nechci tvrdit že jiné řešení neexistují či jsou špatně, ale troufám si říct že goniometricke funkce, jsou na toto nejvíce jednoduché. Takže ne, řešení na úrovni zák. školy mě nenapadá, nepočítám goniometricke funkce.
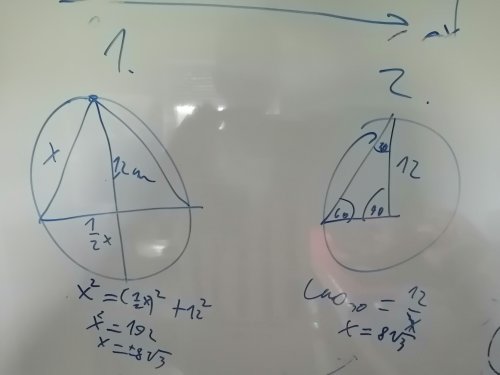
Právě jsem to zkoušel a mám řešení pyhtagorovou větou.
Pythagorova věta v pořádku, jedná se o pravoúhlý trojúhelník, ale nevím odkud jste vzal číslo 12 (co by druhá odvěsna). Prosím o vysvětlení. V zadání příkladu toto číslo není, možná, že mi něco v mých znalostech uniká. Předem děkuji za odpověd.
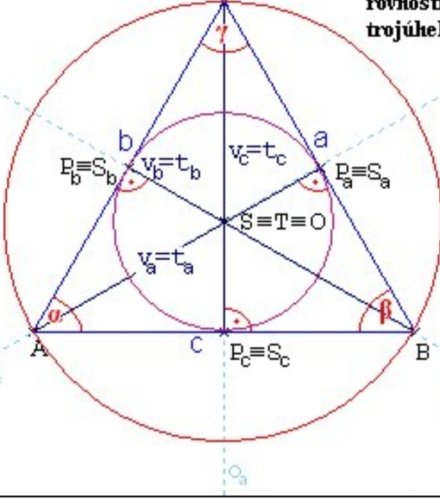
Přikládám obrázek pro rovnostranný trojúhelník ve tvém příkladů, je to pro ten trojúhelník kružnice opsaná. Můžeme jsi všimnout že trojúhelník ABS, (S je střed kružnice) je pravoúhlý. Pak ještě že takové trojúhelníky jse tam vejdou tři. Tudíž 360:3 je 120. Takže úhel v jednom tom velkém trojúhelníku např ABS, je u středu 120, a dokonce je rovnoramenný. Takže ostatní úhly jsou 30, 30. Načež teď ten trojúhelník rozpůlím tak aby měl pravý úhel. Teď můžeme snadno dopočítat úhly. Je to polovina 120, nebo jsi řeknu 120+30+x=180. Takže úhly (trojúhelníku APcS) jsou 30 60 a 90. Pomocí sin30stup. = x/8 dopočítám, že je to 4 cm. A teď vím, že je to 12 cm. Ale samozřejmě že je to vlastně 1,5 násobek poloměru.
Dodatek. Trojúhelník ABS není pravoúhlý, nýbrž APcS.
Protože jsou tětivy stejně dlouhé a svírají 60 stupňů pak se jedná o rovnostranný trojúhelník
jemuž je opsána ktužnice o poloměru 8 cm.V tomto trojúhelníku se výška=těžnice.Víme tedy,
že 2/3 těžnice (výšky) je poloměr kružnice tedy celá výška je 8*3/2=12 cm. Dále použijeme
Pythagorovu větu.
Pánové, moc děkuji za vaše příspěvky. Musím říct, že teprve barevný obrázek narýsovaný kolegou Josefem H. mě přivedl k řešení celého příkladu. Je velice jednoduché.
V rovnostranné trojúhelníku platí výška=těžnice a jednotlivé úhly měří všechny stejně 60°.
Pro výpočet použiji pravoúhlý trojúhelník SBSa a geometrickou funkci cos.
cos 30° = b : c (přepona c je poloměr opsané kružnice 4 cm, odvěsna b je polovina délky tětivy).
cos 30° = b : 4 0.866 = b : 4
b = 3.46 cm
celá tětiva 3.46 x 2 = 6.92 cm (to je správný výsledek pro tento příklad)
Musím upozornit ve znění daného příkladu je dán průměr 8 cm, to znm. že poloměr opsané kružnice je 4 cm.
Ještě jednou děkuji všem za podnětné připomínky.
Ano pardon za ten průměr a ne poloměr :D. Ale postup je správně. Jen jsem špatně četl.
Řešení je tedy správně cos 30 stupňů = 6/x
Řešení je tedy správně cos 30 stupňů = 6/x