Jehlan
Dobrý den, vážení přátelé matematiky, rád bych někoho poprosil o pomoc s tímto příkladem:
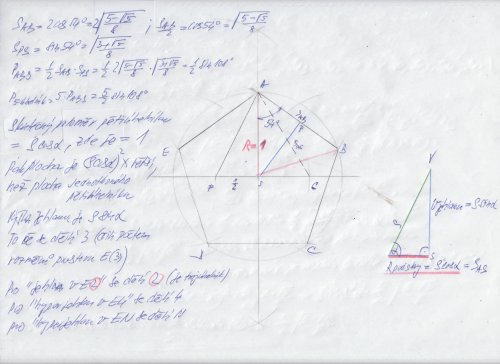
"Určete objem V pravidelného pětibokého jehlanu, má-li jeho boční hrana délku s a je-li alfa odchylka této hrany od roviny podstavy jehlanu."
Podle výsledků by měl být V=0,4 s na třetí sin2alfa cos alfa.
Výška jehlanu mi vyšla v=s*sin alfa (Pythagorova věta), a adále jsem dopočítával, až mi vyšlo řešení V=1,44 s na třetí cos na druhou alfa sin alfa.
Přes veškerou snahu se nemohu dobrat správného výsledku.
Vřelé díky každému, kdo si najde trochu času na odpověď.
S pozdravem Vladimír.
Vladimír J.
07. 10. 2024 14:44
4 odpovědi
Nejprve spočtete plochu jednotkového pětiúhelníku pravidelného, pak tu plochu vynásobíte měřítkovým modulem M ^ 2, kde M = s * cos alfa (protože ta hrana podstavy pětiúhelníku je M * větší, než jednotkového, proto plocha (jednotková) * M ^ 2 . Pak tu plochu znásobíte třetinou výšky jehlanu s * sina alfa a máte objem.
Ještě odvození pětiúhelníku a jeho plochy :
Tak samozřejmě, že lze upravit ( sin alfa ) * ( cos alfa ) na druhou jako jedna polovina * 2 * sin alfa * cos alfa * cos alfa = ( 1/2 ) * sin ( 2 * alfa ) * cos alfa, ale jestli to je "lepší", neřekl bych. To má právě význam u toho úhlu, co fakticky vyjadřuje plochu jednoho trojúhelníku v podstavě pětiúhelníku, čili pět polovin * sin 108° je celý pětiúhelník ( jde totiž vyjádřit algebraicky ), u obecného úhlu alfa obvykle to nepůjde
V tom Vámi uváděném 0.4 je vlastně zakomponován součin 5 / 2 * sin 108 ° * 1/3 * 1/2 * sin 2 alfa cos alfa , čili 5/2 * 1/3 * 1/2 * sin 108° je cca 0.39627, což je asi jako těch Vašich 0.4