Kinematika - padající těleso

Ahoj,

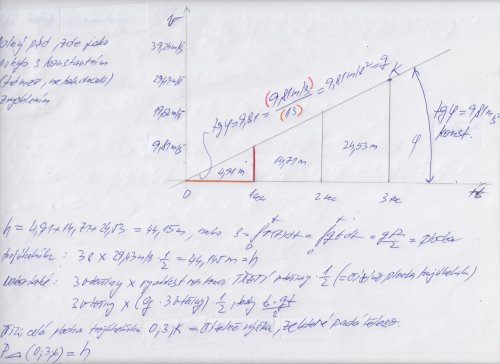
nejdřív zkusím jen napovědět - dráha volného pádu je \( y=\frac{ 1} { 2} gt^2\), tj.

za 1 sekundu urazí dráhu ... \(\frac{ 1} { 2} g\cdot 1\)

za 2 sekundy ... \(\frac{ 1} { 2} g\cdot 4\)

za 3 sekundy ... \(\frac{ 1} { 2} g\cdot 9\)

za \( n \) sekund ... \(\frac{ 1} { 2} g\cdot n^2\)

Pak třeba za 3. sekundu urazí dráhu

\(\frac{ 1} { 2} g\cdot 9-\frac{ 1} { 2} g\cdot 4=\frac{ 5} { 2} g\)

Podobně si vyjádříš dráhu za \( n \)-tou sekundu. Dál by to mohlo být snadné, potíž může být snad jen v obecném vyjádření. (Bez toho by to byla celkem snadná úloha - prostě bychom počítali dráhy za jednotlivé sekundy.)

Ještě může mást označení. Jelikož podle zadání je \( s \) dráha za poslední (\( n \)-tou) sekundu, označil jsem celkovou dráhu \( y \).

Viz níže :

Stále jsem v tom ztracen, mohl bych poprosit o řešení příkladu, snad to z toho pochopím.

Zdravím. Dobře, celý postup:

Jak už ti napsal Miroslav, pro dráhu volného pádu platí \(h=\frac12gt^2\). To znamená, že z výšky \(h\) dopadne těleso za \(t=\sqrt{ \frac{ 2h} g} \)

Podle zadání pak musí platit: \(\sqrt{ \frac{ 2h} g} =\sqrt{ \frac{ 2(h-s)} g} +1\) - (tohle si pořádně promysli, to je klíčová myšlenka)

Tím skončila fyzika a zbytek je algebra na úrovni gymplu.

\(\frac{ 2h} g=\frac{ 2h-2s} g+2\sqrt{ \frac{ 2(h-s)} g} +1\)

\(\frac{ 2s} g-1=\sqrt{ \frac{ 8(h-s)} g} \)

\(\frac{ 4s^2} { g^2} -\frac{ 4s} g+1=\frac{ 8(h-s)} g\)

\(h=\frac{ s^2} { 2g} +\frac s2+\frac g8\)

Ještě doplním svoje řešení - a místo \( n \) budu psát \( t \), což bude lepší:

Za \( t \) sekund urazí \(\frac{ 1} { 2} g\cdot t^2\)

za \( (t-1) \) sekund urazí \(\frac{ 1} { 2} g\cdot (t-1)^2\)

Za poslední sekundu urazí rozdíl těchto vzdáleností, tj.

\(s=\frac{ 1} { 2} g\cdot t^2-\frac{ 1} { 2} g\cdot (t-1)^2= \frac{ 1} { 2} g(2t-1)\)

odkud

\(\displaystyle t= \frac{ s} { g} +\frac{ 1} { 2} \)

Vychází doba pádu 3 sekundy.

Těleso padalo z výšky

\(\displaystyle y= \frac{ 1} { 2} gt^2\)

Máme najít obecné řešení, proto dosadíme

\(\displaystyle y= \frac{ 1} { 2} gt^2=\frac{ 1} { 2} g\left(\frac{ s} { g} +\frac{ 1} { 2} \right)^2\)

což se dá upravit na tvar

\(\displaystyle y= \frac{ (2s+g)^2} { 8g} \)