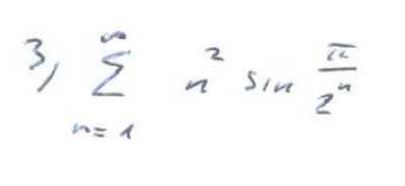Konvergence řady

Př.

Nemůže být, když neznáš tu limitu. Třeba \( \lim_{ n \to \infty} \sqrt[n^2]{ \frac{ 1} { n} } = 1 \) a přitom je to nekonečná odmocnina z nuly.

Máš víc možností, jak ukázat konvergenci, ale nejjednodušší je podílové kriterium, kde využiješ faktu, že \( \sin x \) je roustoucí funkce, tudíž podíl sinů v limitě bude menší než 1.

\( 0 \leq \frac{ (n+1)^2 sin \frac{ \pi} { 2^{ n+1} } } { n^2 sin \frac{ \pi} { 2^n} } \leq \frac{ (n+1)^2} { n^2} \)

A kdyby si pořád nevěděl rady, tak stačí dokázat, že

\( \lim_{ n \to \infty} \frac{ \sin \frac{ \pi} { 2^{ n+1} } } { \sin \frac{ \pi} { 2^n} } = \frac{ 1} { 2} \)

Díky