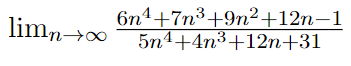Limita postupnosti - dôkaz
Ahojte,
v prílohe mám príklad na výpočet limity postupnosti. Výpočet mi je jasný, všetkému rozumiem. Výsledok je 6/5.
Chcem urobiť dôkaz použitím definície. Viem, čo mám dosadiť do definície.
Problém je v tom, že ďalej sa nepohnem. Ostanem stáť pri nerovnici s absolútnou hodnotou.
Vedeli by ste mi poradiť? Naozaj ma zaujíma, ako pokračovať ďalej :)
Ďakujem.
A. G.
01. 12. 2021 21:49
2 odpovědi
Já bych na to šel postupně - nejprve si vyknu to \(n^4\) a následně limita podílu se rovná podíllu limit. Z definice bych pak dokazoval až ty dvě limity tvořící podíl.
Do nerovnosti pak dám to, co zbyde za šestkou, resp. pětkou proti tomu danému \(\varepsilon\) a spočtu to minimální \(n\)
Výborný nápad, ďakujem!
Ako to vidím:
- V čitateľi i v menovateľi vyjmem pred zátvroku najvyššiu mocninu n-ka.
- Čitateľ i menovateľ je v tváre súčinu - môžeme krátiť.
- Použijeme vetu o podiely dvoch limít. Takto získame limitu postupnosti v čitateľi i limitu postupnosti v menovateľi.
- Na čitateľ i menovateľ aplikujeme vetu o súčte limít. Tým to celé zjednodušíme a vypočítame, že čitateľ má hodnotu 6, menovateľ má hodnotu 5. To znamená, že sme dostali 6/5.
Teraz ten dôkaz. Potrebujem ešte trochu podstčiť...