Lineární nerovnice složitější příklad

Rovnici vyřešíme pro x...

\(x = \frac{ 9-3k} { 5k-10} \)

Následně vyhodnotíme, kdy je výsledek kladný - zlomek je kladný, pokud jsou oba (čitatel i jmenovatel) stejného znaménka, tedy

\( 9-3k > 0\) a zároveň \(5k-10 > 0\), nebo \(9-3k < 0\) a zároveň \(5k-10< 0 \)

Nakonec dostaneme výsledek:

\(k \in (2;3)\)

Detailní postup je jen otázkou vhodných úprav.

A promiňte, že se ještě ptám, ale jaké úpravy musíme udělat, abychom dostali uvedený výsledek ?

První část je učivo základní školy - vyřešit lineární rovnici s jednou neznámou. Jediný rozdíl je, že tam krom čísel máme i písmenko.

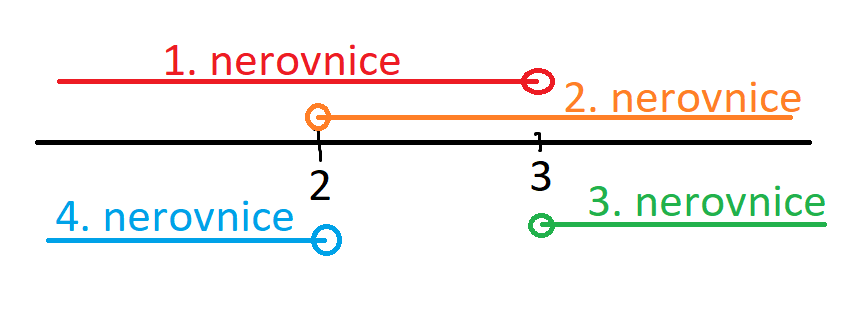
Ve druhém kroku je pak potřeba vyřešit ty čtyři nerovnice pro \(k\) a aplikovat na získané výsledky odpovídající operátory - "a zároveň" přejde v průnik intervalů, "nebo" pak v jejich sjednocení. Nerovnice můžeme řešit stejnými úpravami jako rovnice s jedinou výjimkou - násobení obou stran rovnice záporným číslem otáčí znaménko nerovnosti. Grafické řešení viz příloha.

První dvě nám tedy dají ten výsledek, řešení druhých dvou tvoří prázdnou množinu. Když tyto dva výsledky sjednotíme, zůstane nám ten první.

Dobře začínám se orientovat, ale kdybyste byl tak hodný a vyřešil podrobněji tu rovnici plus následný postup, který vede k výsledku včetně nákresu osy.

Jasně, nechtěl jsem psát rovnou podrobný postup, protože mi přijde, že si lidé na těchto fórech často nechávají řešit domácí úkoly a nemají zájem problematiku pochopit.

V zadání je takzvaná rovnice s parametrem (to k) - řešení nebude číslo, ale nějaký výraz obsahující tento parametr.

Ptají se nás na to, pro jaké hodnoty parametru bude řešení kladné. Jinými slovy - jaká čísla můžu dosadit za k, aby x bylo větší než nula.

Proto z rovnice vyjádříme x. Následně si dáme podmínku, že má být kladné. Výsledkem je zlomek. O libovolném součinu či podílu dvou čísel víme, že bude kladný, pokud budou oba členy kladné nebo oba záporné (+ * + = +, - * - = +, + * - = - * + = -).

To nás přivede k těm nerovnicím - jedna sada řešení je definována prvními dvěma - obojí kladné, druhá dalšími dvěma - obojí záporné. Jak už vyplývá z předchozího odstavce, výsledky získané v dané dvojici musí platit zároveň, výsledky těch dvou dvojic se potom doplňují.

Výsledek řešení jedné lineární nerovnice je obvykle interval od nějakého čísla (bez něj či včetně, závisí na tom, jestli je nerovnost ostrá či ne) k jednomu z nekonečen. V grafickém řešení se to znázorňuje tak, že čára vedoucí do nekonečna se může zakončit šipkou. Konec omezený tím číslem se označí buď plným nebo prázdným kolečkem. Plné je pro případ, že to číslo taky vyhovuje.

Když mám soustavu dvou nerovnic, které mají platit najednou, bude výsledkem překryv jejich řešení (místo, kde jsou ty čáry nad sebou obě). V tom prvním případě tedy interval mezi dvojkou a trojkou. Nerovnosti jsou tam ostré, takže kroužky prázdné, takže do výsledného intervalu ta čísla nespadnou, proto kulaté závorky. Pokud by tam spadala, používá se závorka hranatá nebo špičatá.

Druhý případ nemá čáry nad sebou nikde. Proto je řešením prázdná množina. Nakonec tyto dva případy "slepíme" - je mezi nimi spojka nebo. Jelikož je jeden z intervalů prázdný, slepením získáme ten první interval. Zápis pro výsledek, kdy dostaneme intervaly dva by vypadal následovně:

\(K_1 = (-5;10]\) , \(K_2 = [500;\inf)\), takže \(K = K_1 \cup K_2 = (-5;10] \cup [500;\inf)\)

Případně

\(K_1 = (-5;10]\) , \(K_2 = [10;50)\), takže \(K = K_1 \cup K_2 = (-5;50)\)

já mám zájem to pochopit jen jsem potřeboval postrčit my jsme toto učivo začali brát dnes. Děkuji