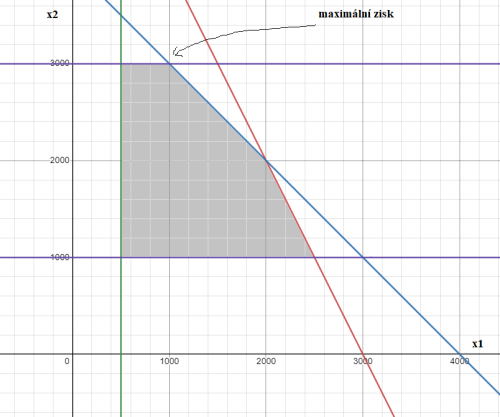
Přepis slovní úlohy do matematického modelu - Lineární programování
Dobrý den, prosím všechny o radu. Potřeboval bych pomoct s přepisem slovní úlohy do matematického modelu (soustava rovnic a nerovnic) v předmětu lineární programování.
Grafické řešení, simplexovou metody i určení vyčerpání omezení umím, bohužel jsem nesprávně vytvořil model a příklad mi nevyšel a nevím jak dál.
Děkuji Všem za případné rady. :)
V dílně firmy specializované na stavební materiály je možné vyrábět čtvercové a obdélníkové pláty. Na čtvercový je potřeba 2 kg speciální hmoty, na obdélníkový 1 kg hmoty, ve skladu je k dispozici celkem 6 000 kg této hmoty. Na odlití a opracování čtvercového i obdélníkové plátu je třeba 1 hodina práce zaměstnance, celkem je k dispozici 4 000 hodin. Odběratel požaduje alespoň 500 kusů čtvercových plátů a alespoň 1 000 kusů obdélníkových plátů, pak se zaručuje odebrat jakékoli množství čtvercových plátů a až 3 000 obdélníkových plátů. Pokud dílna odběrateli prodá všechny vyrobené pláty za smluvené ceny, má z výroby jednoho čtvercového plátu zisk 400 Kč a z jednoho obdélníkového plátu 600 Kč. Stanovte výrobní program, který zaručí za daných podmínek nejvyšší možný zisk.
Alexandr H.
07. 11. 2022 14:50
4 odpovědi
Zdravím.
\(x\) - čtvercové, \(y\) - obdélníkové.
Podmínky: \(0\le2x+y\le6000\)
\(0\le x+y\le4000\)
\(x\ge500\)
\(1000\le y\le3000\)
Zisk: \(Z=400x+600y\)
Dobrý den, děkuji za pohotovou odpověď. Posílám přílohu jak jsem to měl původně. Věděl jsem, že tam ty 3000 musím nějak zakomponovat, ale nevěděl jsem jak. Pak mě napadlo to co jste sem přidal, ale nevím jak bych ze čtvrtého omezení vyjádřil např. grafický zápis, nebo jak s tím dále operovat, např. zapsat toto omezení do simplexové tabulky. Poprosil bych Vás o vysvětlení či přepis do jinačího formátu, jestli mi rozumíte. Posílám jak máme zapsáno my, děkuji. y značíme jako x2, jen pro upřesnění.
Já zase nevím, co je simplexová tabulka, ale graficky to máte na obrázku (šedivě je označená oblast určená podmínkami)
Ahoj,
v příloze jsem převedl problém do kanonické formy. Z té bys měl vidět, jak jednotlivé řádky odpovídají podmínkám, co už sepsal Zdeněk. Konstrukce simplexové tabulky je pak jednoduchá.
Musíš si ale dát pozor na to, že slack proměnné na posledních dvou řádkách jsou surplus (pardon, neznám české ekvivalenty), takže úloha není jednoduchá na řešení. Za základní parametry bys typicky zvolil \( x = y = 0 \), jenže ty nejsou v množině feasible solutions.
V obecném případě je Simplexová metoda nespolehlivá a občas je potřeba intuice nebo vyzkoušet více řešení nebo se podívat do grafu, co nakreslil Zdeněk, abys uhádl, kterou úpravu zvolit.
