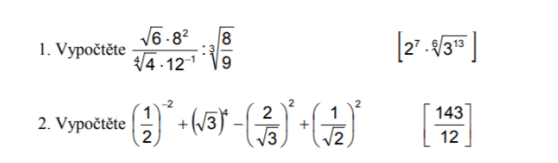Mocniny a Odmocniny - nevíme si rady
Dobrý den, syn dostal ve škole za úkol napsat postup u těchto příkladů, ale já si nevím rady jak mu pomoci. Proto moc prosím, zdali by se našel někdo kdo by mi napsal postup. Závorky vpravo znázorňují finální výsledek.
Děkuji za pomoc.
Karel P.
19. 01. 2022 19:25
3 odpovědi
\(\displaystyle \frac{ 6^{ \frac{ 1} { 2} } \cdot (2^3)^2\cdot 12} { \sqrt{ 2} } \cdot \sqrt[3]{ \frac{ 9} { 8} } \)
\(\displaystyle =\frac{ (2\cdot 3)^{ \frac{ 1} { 2} } \cdot (2^6)\cdot (2^2\cdot 3)} { 2^\frac{ 1} { 2} } \cdot { \frac{ \sqrt[3]{ 9} } { 2} } \)
\(\displaystyle =\frac{ 2^{ \frac{ 1} { 2} } \cdot 3^{ \frac{ 1} { 2} } \cdot 2^8\cdot 3} { 2^\frac{ 1} { 2} } \cdot { \frac{ \sqrt[3]{ 3^2} } { 2} } \)
\(\displaystyle =3^{ \frac{ 1} { 2} } \cdot 2^7\cdot 3\cdot3^\frac{ 2} { 3} \)
\(\displaystyle =2^7\cdot 3^{ 1+\frac{ 1} { 2} +\frac{ 2} { 3} } \)
\(\displaystyle =2^7 \cdot 3^\frac{ 13} { 6} \)
V prvním kroku je využito, že \( 8= 2^3 \) a \( \sqrt[4]{ 4} = \sqrt{ 2} \).
\(\displaystyle \left(\frac{ 1} { 2} \right)^{ -2} +(\sqrt{ 3} )^4-\left(\frac{ 2} { \sqrt{ 3} } \right)^2+\left(\frac{ 1} { \sqrt{ 2} } \right)^2\)
\(\displaystyle =\left(\frac{ 2} { 1} \right)^{ 2} +(3^\frac{ 1} { 2} )^4-\frac{ 2^2} { (\sqrt{ 3} )^2} +\frac{ 1} { (\sqrt{ 2} )^2} \)
\(\displaystyle =2^{ 2} +3^{ \frac{ 1} { 2} \cdot 4} -\frac{ 4} { 3} +\frac{ 1} { 2} \)
\(\displaystyle =4+3^2-\frac{ 4} { 3} +\frac{ 1} { 2} \)
atd., vychází mi jinak, než v uvedeném výsledku
Děkuji za pomoc.