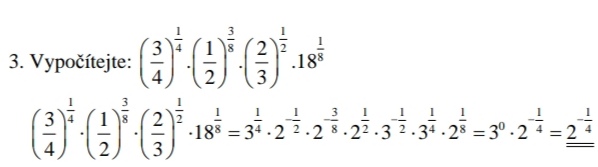Odmocniny a mocniny zlomků

Ahoj, vychází se ze vztahů: \(x^a\cdot x^b = x^{ a+b} \), \(x^{ -a} = \frac{ 1} { x^a} \), \(\left(x^a\right)^b = x^{ a\cdot b} \) a, pokud \(x = y\cdot z\), pak \(x^a = y^a\cdot z^a\) a z toho, že násobení je komutativní - můžu prohazovat pořadí činitelů.

Tedy:

\(\left(\frac{ 3} { 4} \right)^{ \frac{ 1} { 4} } = 3^{ \frac{ 1} { 4} } \cdot 4^{ -\frac{ 1} { 4} } = 3^{ \frac{ 1} { 4} } \cdot 2^{ -\frac{ 2} { 4} } \)

Analogicky ty ostatní členy. Cílem je rozložit to na mocniny prvočísel - budu mít co nejmíň činitelů.

Pak si to přeřadím, abych měl stejné základy vedle sebe a použiju ten vzorec pro násobení.

Možná ještě dodám význam toho zlomku v exponentu: \(x^\frac{ 1} { a} = \sqrt[a]{ x} \)

viz níže