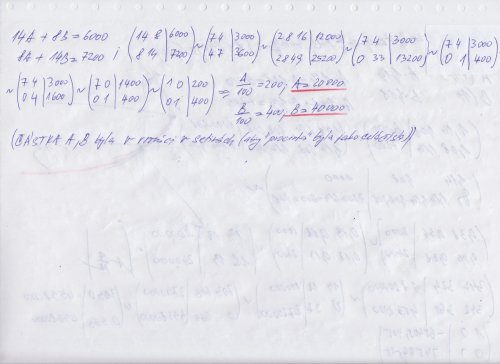Počítání s úroky
Zdravím, vůbec si nevím rady s touto slovní úlohou, pokud by někdo věděl, prosím ozvěte se.
Předem děkuji :-)
Ze dvou částek, ze kterých jedna je úročena čtrnácti procenty a druhá osmi procenty ročně, byl za jeden rok získán
celkem úrok ve výši 6000 Kč. Pokud by se úrokové sazby navzájem vyměnily, dosahoval by celkový úrok za stejné
období hodnoty o 1200 Kč vyšší. Vyšší z původních částek (v Kč) je z intervalu:
a) (27000;32000⟩
b) (32000;37000⟩
c) (37000;42000⟩
d) (42000;45000⟩
e) Žádná z předchozích možností.
Ivo R.
14. 04. 2021 22:56
8 odpovědí
Zdravím.
Podle 1. podmínky \(0,14x+0,08y=6000\)
Podle 2. podmínky \(0,08x+0,014y=7200\)
Stačí vyřešit soustavu.
Oprava: ve 2. je samozřejmě \(0,14y\)
Dobrý den! Nejde se mě vyřešit Vámi napsanou soustavu rovnic kvůli číslam. Mohla bych Vás, prosím, poprosit to rozepsat? Předem děkuji za odpověd.
Dobrý den, řešení je:
0,14x + 0,08y = 6000 /8 0,08x + 0,14y = 7200 /14
1,12x + 0,64y = 48000 1,12x + 1,96y = 100800 =>
1,12x - 1,12x +1,96y - 0,64y = 100800 - 48000 1,32y = 40000 (c)
pokud to uděláme naopak a najdeme x bude se rovna = 20000
to pro nas nejde.
Dobrý deň, a ako je možné tento príklad vyriešiť bez kalkulačky? Tak aby to bolo jednoduchšie? Pretože deliť také číslo 8 a 14 a vôbec, aby ma to napadlo je celkom obtiažné
Dobrý deň, a je to možné vypočítať aj nejako jednoduchšie? Ak by som to musel počítať bez kalkulačky tak ako by som mal postupovať?
Když budete postupovat viz výše, nepotřebujete kalkulačku, máte přehled, co se odehrává, jinak je to vždy jen nepřehledné.