Příklad na shodné zobrazení - translace
Dobrý den, nevím si rady jak narýsovat tento příklad. Budu rád když mi někdo poradí děkuji.
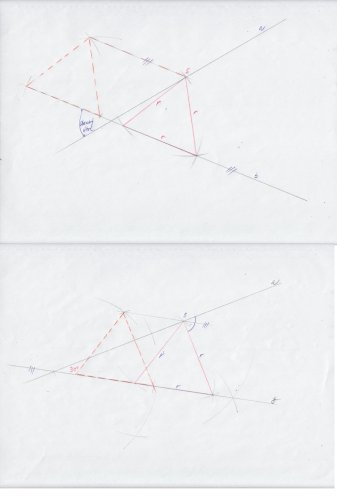
Jsou dány dvě různoběžky a, b a úsečka délky r. Sestrojte všechny kružnice k se středem na přímce a, poloměrem r, které na přímce b vytínají tětivu délky r.
Marek Š.
08. 01. 2024 18:30
5 odpovědí
Ty tři úsečky budou spolu tvořit rovnoramenný trojúhelník a aby se dal sestrojit vrchol na přímce a, který bude středem té kružnice poloměru r, tak bude platit, že ten střed je zároveň patou kolmice na přímku a, takže uděláte rovnoběžku s tou př. a ve vzdálenosti r a ta protne tu b a máte potřebný bod a pak jej spustíte do paty kolmice na a a kružítkem ten poslední bod a máte to, co je požadováno, asi to samé udělate i na druhou stranu
Dobrý den, děkuji za odpověď, jen bych se chtěl zeptat jak bych postupoval kdybych musel užít posunutí (translace) při konstrukci.
Už jsem na to přišel, děkuji za pomoc, moc si toho vážím.
@Milan K., možná špatně chápu tvoji konstrukci, ale ten trojúhelník nejen, že je rovnoramenný, on je i rovnostranný. Ten předpoklad s pravým úhlem pak přesně definuje úhel mezi přímkami, \(30^{ \circ} \). Co tam vidím špatně?
Jinak konstrukce je dle mého následující:
-
Sestrojím rovnostranný trojúhelník o straně \(r\), jehož jedna strana bude ležet na přímce \(b\).
-
Posunu tento trojúhelník tak, aby jeho třetí vrchol ležel na přímce \(a\): narýsuju rovnoběžku s přímkou \(b\) tím třetím vrcholem a tam, kde tato rovnoběžka protne přímku \(a\), bude ten střed kružnice.
-
Výsledky jsou dva, středově souměrné podle průsečíku přímek.