Příklad tuhé těleso
Dobrý den, jako součást domácího úkolu na matematiku jsem dostal tento příklad.
Homogenní dřevěná deska leží na stole tak, že její konec je vysunut o 1/4 její délky mimo stůl, strana desky je rovnoběžná s hranou stolu. Na tento volný konec přiběhne králík. Jakou maximální hmotnost může mít králík, aby se s ním deska nepřeklopila? Hustota dřeva je 600 kg/m^3. Deska je 200 cm dlouhá a 40 cm široká, tloušťka je 2 cm, rozměry králíka zanedbejte.
Je mi jasné, že to bude nějak souviset i s fyzikou, ale díky absenci hodin fyziky kvůli distanční výuce, v tomto příkladu plavu. Za vyřešení budu moc rád a předem děkuji.
Martin K.
13. 05. 2021 12:00
4 odpovědi
Zdravím.
Deska má hmotnost \(m_d=V\varrho=2\cdot0,4\cdot0,02\cdot600=9,6\ \text{ kg} \)
Dále musí platit rovnováha na páce - obrázek - (to je fyzika ze základní školy) \(m_dg\frac l4=m_kg\frac l4\) (\(m_k\) je hmotnost králíka, na obrázku není)
Z toho okamžitě dostáváš, že \(m_k=m_d\)
Snažím se to tady teď pochopit a je tedy výsledek, že maximální hmotnost králíka může být 4,8?
Ne, hmotnost králíka je stejná jako hmotnost desky
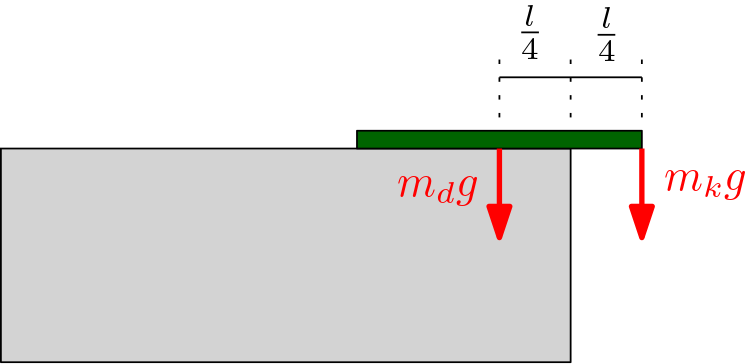
Když se podíváme na obrázek výše, můžeme si úlohu rozdělit (resp. rozdělit tu desku).
Když si desku rozdělíme napůl, bude ta "pravá" část dokonale vyvážená přes hranu stolu.
"Levá" část desky potom bude na páce vyvažovat králíka. Králík na konci bude mít páku délky L/4. Těžiště toho zbytku desky je v jeho prostředku, tedy L/2 od hrany stolu.
To tedy znamená, že králík má poloviční délku ramene páky. Může tedy vážit dvakrát více než to, co ho vyvažuje, což je polovina desky. Může tedy vážit stejně jako deska.