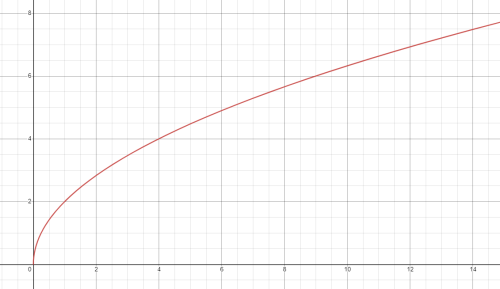
Rychlost v závislosti na dráze
Zdravím,
rád bych si nechal poradit se jedním problémem, se kterým si nevím rady. Zní takto (omluvte případně moji matematickou mluvnici - nejsem odbroník):
Dráha (přímočará), kterou těleso urazí je funkcí času, za který mu to bude trvat: s(t) = t². Zároveň víme, že rychlost (v jakémkoli čase) získáme derivací funkce: v = ds/dt.
Mě by zajímalo, jak bude vypadat graf, kde rychlost v (její hodnota vyznačena na vertikální ose) bude závislá na uražené vzdálenost s (hodnota vyznačena v horizontaální ose).
Za případné odpovědi předem děkuji.
Pavel -.
25. 03. 2021 10:03
2 odpovědi
Zdravím.
Pdle zadání \(v=\frac{ \text ds} { \text dt} =2t\). Z toho \(t=\frac v2\)
Dosazením do dráhy \(s=\left(\frac v2\right)^2\ \Rightarrow\ v=2\sqrt s\)
Fakticky se v tomto případě jedná o pohyb s konstantním zrychlením, pak dráha je integrál v(t)dt < t1,t2>, tedy integrál ct dt = ct^2/2. To se má rovnat u Vás dle zadání 1t^2, z toho pak a(t) = c = a (tak jak se značí coby konstantní zrychlení) =2, čili konstantní zrychlení je zde a=2, čili zde máte a(t) = a = 2m/s^2.
Pak po Vás vlastně chtějí jen znázornit graf, kde místo t na ose X a v(t) na ose Y budete mít již vypočtenou dráhu na ose X a rychlost na ose Y.
Zrychlení může být obecně vždy nějakou funkcí, nikoliv jen konstantní. Takže jelikož pro konstantní zrychlení je dráha druhou mocninou času (krát nějaká zvolená nenulová konstanta, jak je vidět integrací), musí být naopak inverzně rychlost odmocninou z ujeté dráhy. Proto tam máte tu parabolu inversně, jako odmocnina z rychlosti, která zde narůstá lineárně vlivem konstantního zrychlení zde a(t) = a=2m/s^2. Já to značím raději "jinak", protože pak si studenti myslí, že "a" je vždy konstanta a neuvědomují si, že to je obecně funkce času. Tak to (a=konstanta) je jen v určitých případech.