Sestrojte trojúhelník

Dost dobře nerozumím, ten bod, co je patou kolmice k vrcholu A, tedy tam kde končí těžnice ta na straně a, tak má být v polovině délky strany a nebo v polorovině nebo co doopravdy je zamýšleno navíc podivně označen (A od bodu ta) . Když již tak, tak bod je dobré pojmenovat odlišně, než je název těžnice na stranu a, třeba P(ta), jako pata kolmice na straně a daná tou těžnicí.

A dále u té druhé úlohy, máte uvedeno: znám stranu c a pak délku strany a+b (máte velké A) a úhel gamma tedy při vrcholu C . Chce to přesně formulovat, tedy co doopravdy, čili znám jako umístění v rovině stranu c a k tomu její délku a dále jestli je znám pouze součet délky strany a i délky strany b nebo znám stranu a i stranu b tedy u obou délku každé zvlášť či co jiného. Je to dost nejasné, prostě není na škodu říci přesně: znám součet délek stran a+b a nic dalšího. Na tomhle pak silně závisí sestrojení toho trojúhelníku.

Dobrý den, ještě jednou, zcela upřímně u prvního příkladu sama nevim jak s tím naložit, mám pouze zadané, že vím stranu b, vím úhel Beta k vrcholu B a taktéž vím Ta, u druhého příkladu je to přesně jak rikate, vím úhel gamma k vrcholu c, delku strany c a taktéž znam součet délek a+b, veškeré parametry si mohu libovolně určitě a musím to rozepsat tak, jak jsem se snažila v prvním příkladu, bohužel si u té dvojky vůbec nejsem vědoma jak na to…

Dobře, a ten bod, co končí ta těžnice ta je v polovině strany a či jak, máte psáno těžnice ta udává vzdálenost bodu A od bodu ta. Předpokládám, že jste chtěla říci, od bodu na té straně a což je pata kolmice (a nazvla jste jej ta). A dále za tím máte uvedeno : ten se nachází v polorovině strany (kdo, ten bod "ta" alias pata kolmice či nějaký jiný) a dále jaké strany, snad té a, to se musí psát přesně.

Přesně tak, omlouvám se

Pak stačí toto: znáte tedy stranu b (i její délku) a těžnici ta (jen délku), víte, že těžnice končí na straně a pod pravým úhlem čili je to bod paty kolmice. Takže najdete střed strany b a sestrojíte kružnici o poloměru b/2 tzv. Thaletovu a z bodu A sestrojíte kružnici o poloměru ta. Ty kružnice se protnou v bodě, který je tou patou kolmice, tím již znáte dva body úsečky strany a, totiž vrchol C a patu kolmice těžnice ta. Pokud dokonce je ta pata kolmice v polovině délky strany a, tak stačí jen tu polovinu přenést odpichovátkem na druhou stranu a máte B, ale pak ten úhel beta by v tu chvíli byl nadbytečný, nejvýš pro kontrolu, nebo je to prostě jinak zadané.

Toto je mé zadání, s tím, že si mam poradit s příkladem číslo 3 a 11, takže vážně to je zadané takto…

Děkuji mockrát, zkusím se s tim ještě nejak prodrat

Dobře, tak teď je to jasné, takže ale pro tu patu kolmice na straně a platí vše, a to můžete udělat a zakreslit exaktně. Takže neznáme tedy délku strany a ani c, ale to nevadí. Označme patu kolmice ta jako D, pak úsek mezi CD je e a úsek mezi DB (polohu B ještě neznáme) jako e.

Jedná se o pravoúhlý trojúhelník, kde známe těžnici jako přeponu a pravý úhel a úhel beta, čili tři prvky a tím jej známe "ihned" jako celek. Tedy máme již ACD, a chceme jej doplnit na ADB, oba jsou pravoúhlé. Zkusím se podívat, vypočíst a následně sestrojit to jde ihned, ale ten Váš kantor chce tu jednu stranu graficky.

Takže to vlastně mohu vést obdobně jako tady

Kdybych to dělal já, tak po sestrojení dílčího trojúhelníku ACD "někde" na prodloužení strany a, jejíž délku prozatím neznám , JAKO sestrojil pomocný bod B´. V tom bodě bych sestrojil ten volně zvolený úhel beta, já jsem do obrázku dal záměrně 60°(dobře se totiž sestrojuje, je volně volitelný tak proč ne 60°), pod tím úhlem z pomocného bodu B´protahnu rameno a pak mechanicky potahnu rovnoběžku s toutu čarou tak "dlouho" dokud pomocný nástroj (trojúhelník opřený o pravítko" neprojde bodem A. Tím, že sestrojím tu rovnoběžku, tak protne stranu a v bodě B opravdu i úhel bude zachován a to vše s dostatečnou grafickou přesností , podívejte se: vlastně sestrojování rovnoběžek není nic jiného, než primitivní pantograf, co se používal kdysi, když ještě nebyla výpočetní technika a plottery, v geodesii (třeba na katastru, ale jmenovalo se to kdysi středisko geodesie za komunismu), tak sestrojovat rovnoběžky je fakticky na mechanickém principu tzv. paralelogramu, což je to pravítko a o něj "opřený" a posouvající se trojúhelník. Ale samozřejmě, že i rovnoběžky se dají sestrojit exaktně i bez pomocných "mechanických" pomůcek, čistě kružítkem a pravítkem bez značek, podobně i pravý úhel. Tak si to prohlédněte, když tak zkusím tu rovnoběžku s pomocným bodem i "jinak" .

Děkuji mockrát, kouknu na to

A na tu 11 by jste sel prosím jak?

Na to se zkouším právě přijít, zkusím Vám něco poslat, pak to upřesním.

Ještě vám posílám jednou ten 3) jak se to udělá ty rovnoběžky jen s kružítkem. Je to dost přesné a skoro lepší, než tahat čáry s pravítkem a trojúhelníkem = mechanickým pantografem. Prostě z bodu A vezmete od oka nějaký poloměr a přeškrtnete tu čáru ramene beta, to Vám dá dva symetrické body (na rameni beta) a z těch na opačnou stranu vezmete také "o něco" větší poloměr a protnete navzájem oblouky. Ty protnuté oblouky spojíte sbodem A a to protne to rameno úhlu beta, dostanete E. Úplně přesně to samé uděláte nejlépe v bodě B pomocný. Nakonec na tu kolmici jdoucí pomocným bodem nanesete kružítkem AE = B´F. Toto spojíte a máte vyrobenou rovnoběžku co protne CD a na ní "někde je B skutečný. Tak to je celá konstrukce.

Děkuji mockrát

Tam je ten problém, že strana c spolu s úhlem gama a stranami a , b jsou svázány cosinovou větou. Takže nejde "ad hoc" jen tak DOPŘEDU vymyslit třeba gama = 60°, c = 10, a+b = 18. To prostě nevyjde, jen velmi přibližně, ve skutečnosti a+b se bude musit rovnat 18.54 a nekonečně mnoho čísel a to nejde vymyslit, je to irracionální algebraické číslo, naštěstí ne transcendentní, to nejde pak vůbec, takže tohle zvolit, aby to vyšlo exaktně není dost dobře možné. Ve skutečnosti pro gama = 60° c = 10 musí být třeba součet, pokud zvolím třeba a "hezky" = 11, tak b bude irracionální číslo, totiž (11+odmocnina ze 37)/2 ,takže a+b = 11 + (11+odmocnina ze 37)/2 proto nejde od oka takovouto konfiguraci zvolit. Prostě říci si: c = 10 , pak a+b = 18 úhel gama třeba 30° nejde realizovat. Vždycky ten součet a+b bude iracionální číslo, které bude dáno ve tvaru odmocnin a ty nejde "vymyslit", ty se počítají. Jedině, kdy by to jakž takž fungovalo tak když to bude rovnoramený trojúhelník gama =301 nebo rovnostranný, nebo pravoúhlý, tam se totiž stane to, že ten člen s cos 90°se zruší a strany mohou být v součtu "jako hezky", třeba c=5 , a+b=7, gama =90° (což bude vyhovovat jediné konfiguraci a=3,b=4. zkrátka tohle ad hoc jen tak zadat povede k tomu, že to bude vesměs neřešitelné, nevyhoví to cosinové větě. V případě rovnostranného trojúhelníku to pak vyjde ale tak, že třeba c= 10 , a+b=20 , gama = 60°, tak tam se ten smíšený člen vyruší. Ad hoc ale vymyslit z hlavy součet, který je dán iracionálním číslem ale nejde (neznáme nekonečně mnoho číslic). A navíc, pokud to bude úhel gama obecný, tak pokud nebude tzv. fermatovský, tak tím hůře, pak to bude ten součet a+b vycházet dokonce transcendentně, čili nepůjde vyjádřit konečným počtem algebraických úkonů, prostě cosinus obecného nefermatovského úhlu nejde "udělat", stačí třeba takových gama = 40° a je konečná. Pak a+b je doslova transcendentní číslo čili nejen iracionální ale ani algebraické. Takže zde nevím, mohu vám jedině zkusit takovou konfiguraci, co bude vycházet, jenže se musí stanovit ten součet a+b cosinovou větou a s "hezkým" úhlem = fermatovským. S úhlem obecným bude a+b vždycky trancendentní číslo, nebo naopak ta strana c bude transcendentní číslo a pak bude a+b jako "hezky" vyjádřitelné. Nevím, jestli si tohle Váš učitel vůbec uvědomil, bylo by dobré, aby Vám ad hoc, když to tedy chce, zadal nějaké konkrétní hodnoty a Vy cosinovou větou prověříte, že to nejspíše nepůjde.

Našla jsem toto, zda by to neslo nejak překopat a z vc udělat pouze c, ale nevím, zcela upřímně jsem z toho úplně mimo a u předešlého nevim (u té 3) co napsat do diskuze :/

Obávám se, že to z toho nepůjde. Zde známe vrchol C a úhel gama, ten lze sestrojit (ale je dán obecně, tak jedině úhloměrem), tím máte ramena, na kterých leží strany a, b, a dále známe c. Za předpokladu, že ty všechny veličiny splňují cosinovou větu, tj, výpočet viz níže, tak to bude sestrojitelné. Třeba vyrobil jsem pár konfigurací, které jdou a od kdy to pak nejde, ale zpaměti je vyrobit je dost nemožné, (tak propočítávat "z hlavy" vliv cosinu úhlu je dost složité) a spolehnout se na trojúhelníkovou nerovnost zde nestačí, ta je sice nutná ale závisí dále na tom úhlu. Jenže aby to šlo graficky sestrojit, tak musíme vlastně graficky vyřešit kvadratickou rovnici pro neznámou stranu a. Vyjdou dva kořeny a1, a2 a ty v součtu se rovnají a+b, což znamená že a1 je například a pak a2 je zároveň b a nebo přesně naopak, je to zrcadlově symetrické. Takže celý problém je, jak řešit z grafických hodnot kvadratickou rovnici graficky. Pokud to jde, získáme naráz a i b pak stačí ty hodnoty vzít do kružítka a je vyřešeno, c bude mezi nimi "pasovat". viz níže : Když tak až zítra večer. Celý problém je prostě to, jak z délky a+b a délky c, obojí máme graficky na papíře, jak sestrojit neznámou délku a, což je grafické řešení kvadratické rovnice, tím mám na mysli ne řešení, kdy se nakreslí kvadratická funkce, ale kdy se nakreslí jen délka a+b, pak do kružítka délka c na thaletově kružinici je pata kolmice, odkud máme délku odmocnina ((a+b)^2-c^2) a tak podobně s dalšími potřebnými hodnotami.

Tak ten příklad č. 3 bude jinak, celou dobu jsem si myslil, že se jedná o výšku na stranu a, je to těžnice a její koncový bod je v polovině délky strany a. Takže konstrukce bude poněkud složitější. Zítra se Vám podívám. To ode mne by se vztahovalo, kdyby se jednalo o výšku na stranu a. Tak se omlouvám, nějak jsem si toho nevšiml.

Dobře i tak mockrát děkuji

Nejak jsem to zkusila, sama jsem zvědavá, co mi na to pan magistr odpoví

Ahoj,

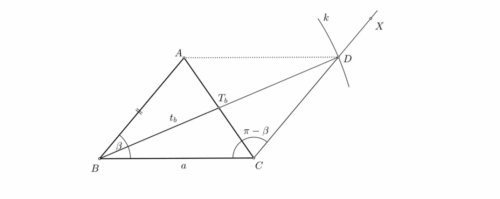
k té úloze 3), tedy zadané \(b,\beta,t_a\):

Úvaha - když si tu těžnici protáhnu i na druhou stranu za střed strany a, dostanu rovnoběžník. Ten je středově souměrný podle středu strany a.

Postup:

1. úsečka \(AD: |AD| = 2t_a\), bod \(S_a\)... střed úsečky \(AD\)
2. kružnice \(k_b\), střed v bodě \(A\), poloměr \(b\)
3. dva kružnicové oblouky \(k_\beta\) - množina bodů, ze kterých je úsečka \(S_aD\) vidět pod úhlem \(\beta\) (postup viz níže)
4. bod \(C \in k_b \cap k_\beta\)
5. bod \(B: B \in \) přímka \(CS_a \land |BS_a| = |CS_a|\)

Množina všech bodů, ze kterých je úsečka \(XY\) vidět pod úhlem \(\alpha\):

1. osa úsečky \(XY = o\)
2. úhel \(\angle AXY: |\angle AXY| = \alpha\)
3. přímka \(p: X \in p \land p \perp AX\)
4. bod \(S \in p \cap o\)
5. oblouk \(k_\alpha: \) střed \(S\), poloměr \(|SX|\)

Pro \(\alpha > 90^\circ\) beru ten kratší oblouk mezi body \(X\) a \(Y\), pro zbytek ten delší. Konstrukci bych měl udělat symetricky na obě strany, abych dostal celou množinu - oba oblouky.

Jeee děkuji, mockrát

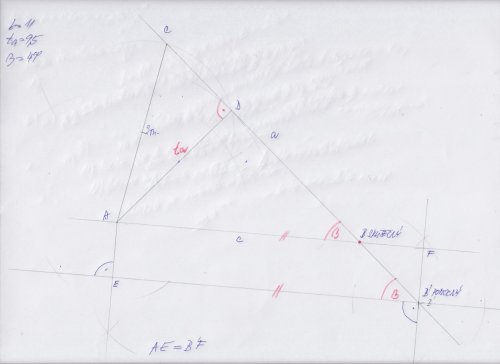
Nevím, jestli se tu už dořešila 11) \(a+b, c, \gamma\), ale postup bych viděl s nápovědou o podobné úloze takto:

1. úsečka \(BA': |BA'| = a+b\)
2. úhel \(\angle BA'X: |\angle BA'X| = \gamma/2\)
3. kružnice \(k_c: \) střed \(B\), poloměr \(=c\)
4. bod \(A \in k_c \cap \) polopřímka \(A'X\)
5. přímka \(o\) - osa úsečky \(AA'\)

alternativně 5) množina všech bodů, ze kterých je úsečka \(AB\) vidět pod úhlem \(\gamma\).

6. bod \(C \in BA' \cap \) výsledek bodu 5

Nejak takto jswm na to šla, tak se uvidí, co mi přijde za opravu, děkuji mockrát, kdyztak se ještě ozvu