Určení polohy přímky s parametrem vzhledem ke kružnici
Potřeboval bych pomoct s tímto příkladem:
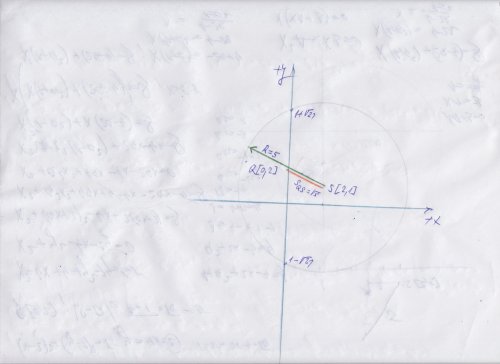
Je dána kružnice \(k: \left (x-2 \right )^{ 2} + \left (y-1 \right )^{ 2} =5\) a přímka \(p: y=ax+2\). Určete, pro které hodnoty reálného parametru a je přímka p tečnou, sečnou a pro které vnější přímkou kružnice k.
Postupoval jsem tak, že jsem rovnici přímky dosadil do rovnice kružnice, to mě dovedlo k diskriminantu, ze kterého mi vypadla lineární rovnice a nakonec špatné řešení viz. foto...
Děkuji za odpověď.
Vojtěch T.
28. 06. 2023 16:25
7 odpovědí
Ahoj,
chybička je ve výpočtu diskriminantu, přesněji jeho druhé části.
Nápověda: Rozmysli si, co v obecné kvadratické rovnici \( ax^2+bx+c=0 \) je v tomto případě \( a, b, c \).
Na první pohled je vidět, že přímka bude vždy sečnou, jelikož : úsek který vytíná přímka na ose Y = 2, (tedy bod Q [ 0,2 ] má vzdálenost od středu S [ 2 ,1 ] , │SQ│ = odm. z 5 a to je menší, než R = 5. Takže aby bylo co s hlediska parametru "a" určovat, je nutné nejprve zjistit, jaká je vzdálenost průsečíku přímky s osou Y od středu kružnice. Pokud je menší, nemá žádný smysl zjišťovat, pro jaký parametr bude tečnou či vnější přímkou, když jí být prostě nemůže a bude to vždy sečna. Takže postup by měl být následující, nejprve zjistit, jaká je poloha úseku na ose Y vůči středu kružnice , pokud bude právě rovná poloměru ( pak Qy = 1 + odm. 21 nebo Qy = 1 - odm. 21 ), tak může být tečnou i sečnou , pokud větší, než poloměr kružnice (pak bude Qy > 1+odm. 21 nebo Qy < 1 - odm 21) , může být sečnou, tečnou i vnější přímkou, pokud menší než poloměr, může být pouze sečnou. Takže jelikož výše uvedená přímka může být pouze sečnou (jelikož takto zadána prochází bodem Q [ 0 , 2 ] uvnitř kružnice ) , což lze velmi snadno zjistit i bez výpočtu, je výpočet přes dosazování do rovnice kružnice již neúčelný.
Jestli dobře počítám, přímka je pro určitou hodnotu parametru tečnou, pro ostatní hodnoty parametru je sečnou.
Pro kontrolu může být užitečný (správný) náčrt kružnice, dále bodu na ose y, kterým vždy prochází přímka (z rovnice přímky) - a pak načrtnout několik různých přímek.
@Milan K. - ve středové rovnici kružnice je na pravé straně druhá mocnina poloměru. Ten je tedy \(\sqrt{ 5} \) a může to tedy být i tečna.
Ano, myslil jsem, že tam vidím 5^2, bylo to (odmocnina z 5) na druhou, tedy přímo 5. Takhle to je ten druhý případ, kdy bod na ose Y je od středu kružice roven poloměru tedy odmocnině z 5 čili může být tedy sečna i tečna.
Děkuju za odpevědi, úplně jsem přehlédnul tu chybu v diskriminantu.
Naprosto zbytečnè to řešit diskriminantem, když chybí absolutní člen. Vytkneme x a hned vidíme, že jsou vždy dvě řešení, kromě případu, kdy koeficient u x je nulový, tj a=2.