Sinus a úhel

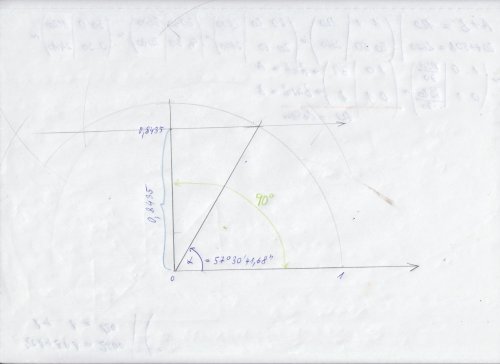
Snadno, nakreslete si čtvrtkružnici o R=10 cm a vodorovnou osu, jdoucí středem a na ni kolmo svislou osu, také jdoucí středem. Od středu si naneste 84.35 mm na tu svislou osu a v místě toho bodu udělejte rovnoběžku s tou vodorovnou osou a kde protne ten oblouk té čtvrtkružnice, tak ten průsečík spojte se středem té kružnice a máte realizovaný úhel, který tomuto sinu alfa odpovídá. Pak jej nějak odměřte a máte jej, tak na 10 šedesátinných minut na papíře. Vyjde vám cca 57°40´, přesněji arcsin .8435 = 57°30´41.68", když budete mít grafický program, (třeba geodetický) tak to budete mít třeba na šedesátinné vteřiny (pracuje v libovolně nastavených v souřadnicích na poměrně velký počet desetinných míst , ikdyž ty souřadnice "nevidíte")

@Milan to hezky popsal, jak se to dá udělat graficky.

Pro středoškolskou aplikaci je asi ještě zajímavé, jak s tím pracovat na kalkulačce...

Je potřeba použít tzv inverzní funkci k funkci \(\sin\), tedy "arcsin", "asin", nebo třeba "\(\sin^-1\)", záleží na konkrétní kalkulačce.

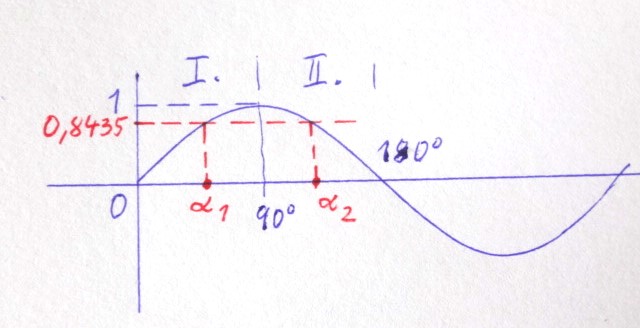
Sinus je funkce, která "sežere" úhel a "vyplivne" číslo mezi \(-1\) a \(1\) - viz grafické řešení.

Inverzní funkce je taková, která "sežere" ten výsledek, tedy číslo mezi \(-1\) a \(1\) a "vyplivne" ten odpovídající úhel.

Jen ještě pozor, aby byla kalkulačka nastavená na správné úhlové jednotky, které se po vás chtějí.

ahoj,

jen doplním, že úloha má dvě řešení:

• v I. kvadrantu (57°30´ nebo přesněji 57°31´)

• ve II. kvadrantu: 180° – 57°30´ = ...

neboť číslo 0,8435 je kladné a funkce sinus má kladné hodnoty v těchto dvou kvadrantech (viz obr.)