Úloha zachovaní rovnováhy
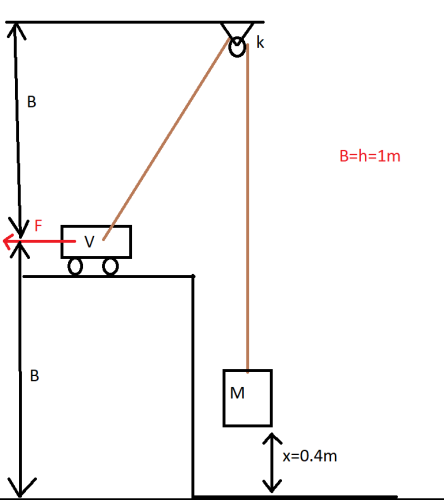
Dobrý den, dokázal by mi někdo ukázat postup u následujícího příkladu se zadáním : Závaží o hmotnosti m je spojeno s vozíkem v o hmotnosti mv lanem o délce l=2b+h, které prochází přes malou kladku k. určete velikost síly f, kterou je možno soustavu udržet v rovnováze. Vyjádřete v závislosti na poloze x závaží M. Zbylé údaje viz obrázek. Předem děkuji za ochotu
Jan K.
06. 06. 2023 12:10
3 odpovědi
Zdravím.
Než začnu budu předpokládat, že síla \(F\) má být vodorovná, tak, jak je to na obrázku. Z textu zadání to není úplně jasné.
Jelikož je soustava v rovnováze, napětí v lanku \(T\), které drží závaží \(M\), musí být rovno tíze tohoto závaží.
\(T=Mg\)
jinak by ten vozík nezůstal na stole (nebo co to je).
Dále, toto napětí je v celém lanku stejné. To znamená, že pro vozík ve vodorovném směru platí
\(F=T\cos\alpha\),
kde úhel \(\alpha\) je úhel mezi úsečkou \(VK\) a vodorovným směrem. Ve svislém směru navíc platí podmínka
\(m_vg\ge T\sin\alpha\)
Určíme délku \(|VK|=a=l-(2b-x)=2b+h-2b+x=h+x\).
Platí \(\sin\alpha=\dfrac ba=\dfrac b{ h+x} =\dfrac 1{ x+1} \), když jsme využili číselné hodnoty za zadání. A
\(\cos\alpha=\sqrt{ 1-\sin^2\alpha} =\dfrac{ \sqrt{ x(x+2)} } { x+1} \)
Postupným dosazením dostaneme
\(F=Mg\dfrac{ \sqrt{ x(x+2)} } { x+1} \) za podmínky \(m_v\ge\dfrac M{ x+1} \)
dobrý den vše je mi jasné jen nechapu ten cos. prilehla ku odvesne to není a kdybych chtěl počítat přes pythagorovu vetu bylo by to \(\sqrt{ { a} ^{ 2} -{ b} ^{ 2} } \)
dekuji za vysvetleni
Zdravím.
Ano, přes Pythagorovu větu to určitě počítat můžete \(\cos\alpha=\dfrac{ \sqrt{ a^2-b^2} } { a} \).
Já jsem použil goniometrickou jednotku \(\sin^2\alpha+\cos^2\alpha=1\)
Vyjít to musí stejně.