Výpočet extrému pomocí derivací
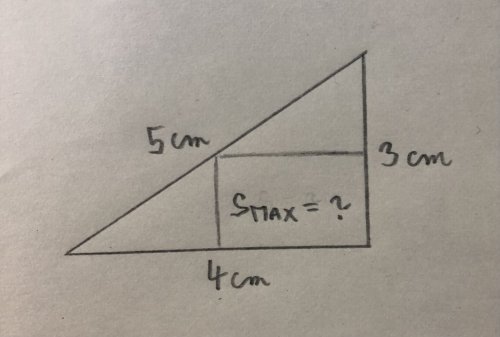
Jak vypočítám největší možný obsah obdélníku v pravoúhlém trojúhelníku o rozměrech 5, 4, 3?
Maria L.
15. 10. 2021 18:14
2 odpovědi
Zeněk R.
16.10.2021 12:49:24
Zdravím,
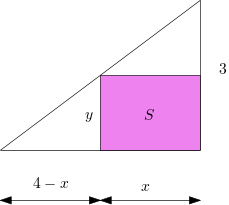
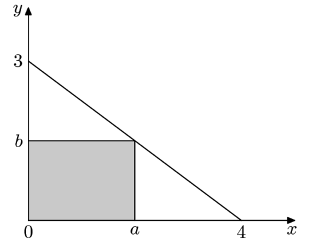
Jednu stranu obdélníka si označíš \(x\) a druhou \(y\). Potom z podobnosti trojúhelníků (obrázek) plyne \(\frac y{ 4-x} =\frac34\ \Rightarrow\ y=3-\frac34x\)
Obsah obdélníka je \(S=xy=x\left(3-\frac34x\right)=3x-\frac34x^2\)
Vypočítáš si derivaci a položíš ji rovnu nule
\(S^\prime=3-\frac32x=0\ \Rightarrow\ x=2\) (Jedná se o maximum. To je triviálně vidět z toho, že jde o kvadratickou funkci se záporným koeficientem u kvadratického členu)
\(S_{ max} =S(2)=3\cdot2-\frac34\cdot2^2=3\)
Pro napsání komentáře se musíte přihlásit.