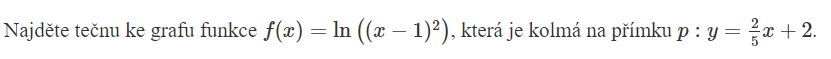Výpočet tečny ke grafu funkce

Rovnice přímky má tvar $y=kx+q$, kde $k$ je směrnice.

Tečna má být kolmá k přímce $p$. Přímka $p$ má směrnici $k_1=2/5$. Pro směrnice kolmých přímek platí $k_1\cdot k_2=-1$, odtud vypočítáme směrnici tečny $k_2$.

Rovnice tečny pak je $y=k_2 x+q$, kde konstantu $q$ zatím neznáme.

Zároveň ale platí, že derivace funkce tečny v daném bodě je rovna směrnici tečny. Proto zderivujeme zadanou funkci a její derivaci položíme rovnu $k_2$. Odtud vypočítáme souřadnici $x_0$ bodu dotyku. Z rovnice funkce dopočítáme hodnotu $y_0$.

Souřadnice $x_0 , y_0$ dosadíme do rovnice tečny $y=k_2 x+q$ a vypočítáme konstantu q.

Bod o souřadnicích $x_0 , y_0$ je bodem dotyku tečny a grafu funkce, leží tedy jak na grafu funkce, tak na hledané tečně.

Stačí takto?

Vloudila se chybička - 4. odstavec má být:

Zároveň ale platí, že derivace funkce v daném bodě ...

Dokonalý, děkuji moc. Teď už bych to měl dát dohromady :)