Zrychlení tělesa
Dobrý den,
Mohl by mi někdo prosím ukázat řešení následující úlohy? Předem děkuji za ochotu.
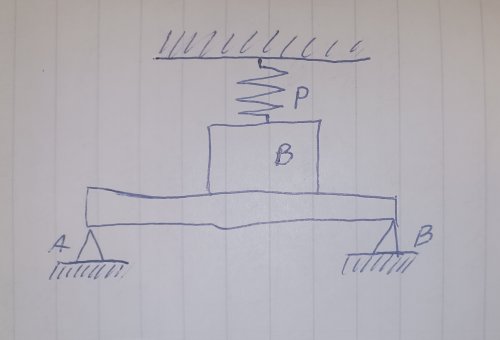
Na nosník hmotnosti m2 je položeno břemeno o hmotnosti m1 a je na něj přitlačováno
silou P. Nosnik leží na dvou podporách A a B. Určete tlakovou silu D mezi břemenem a
nosníkem v okamžiku současného odstranění obou podpor A a B. Jaké bude zrychleni
pohybu obou těles? m1 = 10 kg, m2 = 20 kg, P=400 N.
Jan K.
07. 06. 2023 00:42
3 odpovědi
Je ale nezbytně nutné uvést, jak geometricky a polohově jsou těžiště těch břemen m1, m2 a působící síla vůči podpěrám situovány. Jsou to vlastně dvě spojitá zatížení a jedna osově působící síla. Tedy, zda je vše v jedné ose a navíc symetricky vůči A, B. To je důležité. Protože na tom velmi záleží reakce v podpěrách .
Dobrý den,
Pro její řešení je potřeba znát některé zákony a principy, jako jsou rovnováha sil, moment síly, tlaková síla a zrychlení.
- Nejprve musíme určit reakční síly podpor A a B, když je břemeno přitlačováno silou P. To uděláme pomocí rovnováhy sil a momentu síly. Označme reakční síly podpor A a B jako R_A a R_B. Pak platí:
R_A + R_B = P + m_1 g + m_2 g (rovnováha sil ve svislém směru)
R_A L = P L/2 + m_1 g L/2 + m_2 g L/4 (rovnováha momentu síly kolem bodu B)
Odtud vyjádříme R_A a R_B:
R_A = (P + m_1 g + m_2 g)/2 - m_2 g L/4
R_B = (P + m_1 g + m_2 g)/2 + m_2 g L/4
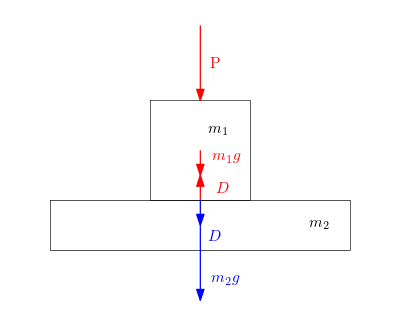
- Potom musíme určit tlakovou sílu D mezi břemenem a nosníkem v okamžiku současného odstranění obou podpor A a B. To uděláme pomocí rovnováhy sil na břemenu. Označme zrychlení břemena jako a. Pak platí:
P - D - m_1 g = m_1 a (rovnováha sil na břemenu ve svislém směru)
Odtud vyjádříme D:
D = P - m_1 g - m_1 a
- Nakonec musíme určit zrychlení pohybu obou těles. To uděláme pomocí rovnováhy sil na nosníku. Označme zrychlení nosníku jako A. Pak platí:
D - m_2 g = m_2 A (rovnováha sil na nosníku ve svislém směru)
Odtud vyjádříme A:
A = (D - m_2 g)/m_2
Dosadíme za D výraz z bodu 2):
A = (P - m_1 g - m_1 a - m_2 g)/m_2
Protože obě tělesa jsou spojena nosníkem, musí mít stejné zrychlení, tedy a = A. Dosadíme za A výraz z bodu 3):
a = (P - m_1 g - m_1 a - m_2 g)/m_2
Upravíme rovnici pro a:
a (m_1 + m_2) = P - (m_1 + m_2) g
a = (P - (m_1 + m_2) g)/(m_1 + m_2)
To je finální výsledek pro zrychlení pohybu obou těles.
Pokud dosadíme číselné hodnoty do výsledných vzorců pro D a a, dostaneme:
D = 400 - 10 * 9,81 - 10 * ((400 - (10 + 20) * 9,81)/(10 + 20)) N
D = 98,8 N
a = (400 - (10 + 20) * 9,81)/(10 + 20) m/s^2
a = 6,53 m/s^2
|<--L-->| | | | | | | | | | | | | P | | | | | V | | m1 | |_____ | /
| /
| /
| /
| /
| / \
A/ \B
Kde A a B jsou podpory, L je délka nosníku, P je síla působící na břemeno, m1 je hmotnost břemena a m2 je hmotnost nosníku. Reakční síly podpor A a B jsou označeny jako R_A a R_B.