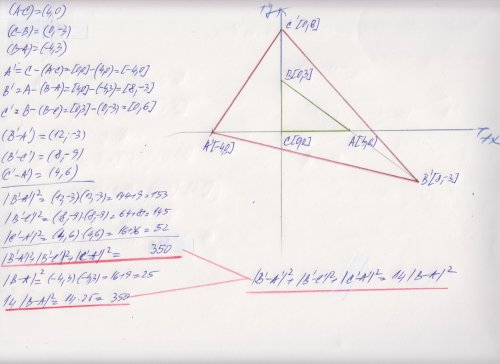
Analytická geometrie - ověření platnosti rovnice
Trojúhelník ABC je pravoúhlý s pravým úhlem při vrcholu C. Body A', B', C' jsou obrazy bodů A, B, C postupně ve středových souměrnostech se středy C, A, B. Dokažte, že platí
|A'B'|² + |B'C'|² + |C'A'|² = 14. |AB|² .
Prosím nevíte, jak to dokázat?
Filip R.
03. 01. 2024 22:24
6 odpovědí
Viz níže :
Já bych spíš potřeboval, obecnou platnost, pro všechny trojúhelníky. Zkrátka abych po úpravě rovnice dostal např. a=a
Zkrátka řešit to pouze jako rovnici bez hodnot a přesných pozic bodů.
Tak jistě, stačí dosadit obecné hodnoty, ale i tak, pro lepší odvozování to umístit do počátku a do os X,Y, jinak by tam na vyjadřování souřadnicových rozdílů figurovalo přiliš veličin, takhle budou mít jednodušší tvar (bude se odečítat více nul)
Viz níže, do obrázku si všude jen přepište, místo konklrétních souřadnic ty obecné . To samé vyjde, ale o dost rozsáhlji zapsané, kdyby to bylo v obecném místě roviny X,Y.
Ještě jeden řádek (úplně dole) , aby bylo vidět, co se porovnává. To samé vyjde, ikdyby byl trojůhelník natočen a v jiném místě umístěn, jen to bude pracnější (budou tam dvojčleny na druhou).
