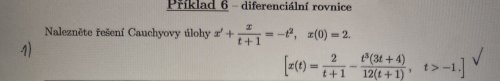Diferenciální rovnice
Zdravím, rád bych se zeptal jak se řeší tento příklad a co vlastně znamená Cauchyho úloha. Pokud jsem to dobře pochopil, tak to znamená pouze to, že má rovnice ještě počáteční podmínku. Děkuji moc za vysvětlení.
Jan N.
13. 08. 2023 16:16
5 odpovědí
Tohle je takový dosti nešťastný způsob značení, fakticky se obvykle značí funkce y = y(x) , takže to co je tu jako x´ je vlastně y´, a x ( 0 ) je vlastně y ( x = 0 ) . Celých 200 - 300 let to nevadilo a někdo má zapotřebí vymýšlet nové značení. Je to zcela zbytečně zmatečné. Zejména, když se něco řeší provedením separace proměnných, jelikož "y" si "zakázali", pak je problém napsat dy/dx a je třeba vymýšlet uměle naprosto zbytečně jiné značení.
Cauchyovou úlohou (počáteční úlohou) pro diferenciální rovnici
F ( x, y, y′ ) = 0 označujeme úlohu y′ = f (x, y ) , y ( x0 ) = y0 .
Řešením Cauchyho úlohy je takové řešení y = y ( x ) diferenciální rovnice, které je definováno na nějakém intervalu I a splňuje počáteční podmínku y ( x0 ) = y0 ( kde x0 ∈ I ) .
Značení, které je tu užito, je ale tradiční
Děkuji, ještě se pro jistotu zeptám, tuto konkrétní úlohu řeším separací proměnných. Je to homogenní rovnice
y´=f(x/y)? Moc to v tom totiž nevidím.
Toto je klasické značení motivované fyzikou, kde x(t) obvykle značí vývoj x-ové souřadnice v čase t. Derivace x podle t je pak klasicky dx/dt. Jinak co se týče řešení, je to lineární dif. rce, takže je třeba nejdříve řešit homogenní rci a pak pomocí variace konstanty najít obecné řešení.
Tak za předpokladu, že "jejich" x je t pak je to velmi jednoduché viz níže :
ale značím to klasicky, není jen fyzika, "dešifrovat" označení se dá jak vidět níže, až na konci .
