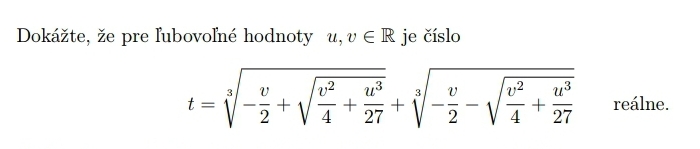Dokázať, že výsledkom cardanovho vzorca bude vždy reálne číslo, napriek dosadeniu ľubovoľných konštánt.

Ahoj, příklad rozdělíme na případy zjevné, případ, kdy je potřeba obezřetnost a případ, kdy je potřeba dokazovat.

1. \(u=0, v\neq0\)

pod 2. odmocninou je zaručeně kladné číslo \(\frac{ v^2} { 4} \), tudíž je vše v pořádku

2. \(u>0, v\neq 0\)

opět, pod 2. odmocninou je zaručeně kladné číslo.

3. Jediný problematický případ: \(u<0, v\neq0\)

nezáporné číslo pod 2. odmocninou dostaneme pouze pro \(-u \leq \sqrt[3]{ \frac{ 27} { 4} v^2} \)

Nyní se tedy zaměřme na případ, kdy pod druhou odmocninou vznikne záporné číslo.

\(t = \sqrt[3]{ -\frac{ v} { 2} + i\sqrt{ \left|\frac{ v^2} { 4} + \frac{ u^3} { 27} \right|} } + \sqrt[3]{ -\frac{ v} { 2} - i\sqrt{ \left|\frac{ v^2} { 4} + \frac{ u^3} { 27} \right|} } = \sqrt[3]{ a + ib} + \sqrt[3]{ a-ib} \), kde \(a,b > 0\)

Pomocí exponenciálního tvaru můžeme přepsat na

\(t = \sqrt[3]{ \sqrt{ a^2 + b^2} } \cdot \left(e^{ i\frac{ atan \frac{ b} { a} } { 3} } + e^{ i\frac{ atan \frac{ -b} { a} } { 3} } \right)\)

První člen je reálný, stačí tedy dopočítat závorku.

\( = \left(e^{ i\frac{ atan \frac{ b} { a} } { 3} } + e^{ -i\frac{ atan \frac{ b} { a} } { 3} } \right)\) = e^{ ix} + e^{ -ix} \)

Dostáváme tedy součet dvou komplexně sdružených čísel, který je z definice reálný, konkrétně dostaneme ze závorky hodnotu \(2 \sin(x)\). Celkový výsledek tedy lze zapsat jako součin reálných čísel, který je z definice také reálný.

Úplně detailní řešení by ještě mělo být přenásobené \(e^{ \frac{ 2} { 3} k\pi i} \). Tento člen vygeneruje další dvě, komplexně sdružené řešení, která už reálná nebudou.

Dobrý deň,

veľmi pekne ďakujem. Dôkaz mi je už viac-menej zrejmejší, lenže časti kde pri exponente eulerovho čísla máte "atan", nerozumiem. Nedá sa argument "fí" opísať aj inou funkciou?

Ešte raz ďakujem za pomoc.

Prajem pekný deň.

Atan je jedna z používaných zkratek pro inverzní funkci k funkci tangens.

Definice argumentu "fi" touhle cestou vychází ze zobrazení komplexních čísel v rovině a převodu do polárních souřadnic.

Například číslo \(2+i\) převedeme na \(\sqrt{ 5} e^{ i\varphi} \). V rovině má toto číslo souřadnice \([2,1]\), tedy \(\varphi = \arctan \frac{ 1} { 2} \).

Ďakujem, veľmi pekne ďakujem za pomoc.

Ešte som postrehol, že pravdepodobne pri Atan-e ste sa pomýlil a Atan mal byť definovaný ako

\(atan\frac{ a} { b} \)

Či sa mýlim?

Avšak v konečnom dôsledku je celý dôkaz v poriadku. Ešte raz ďakujem za objasnenie.

\(\varphi = \arctan \frac{ \Im(z)} { \Re (z)} \) - protilehlá ku přilehlé. Čili si myslím, že to mám dobře, jelikož a je reaálná část a b je imaginární.

Ospravedlňujem sa, vzájomne som si zamenil tieto dve odvesny.