Komplexní číslo na nultou

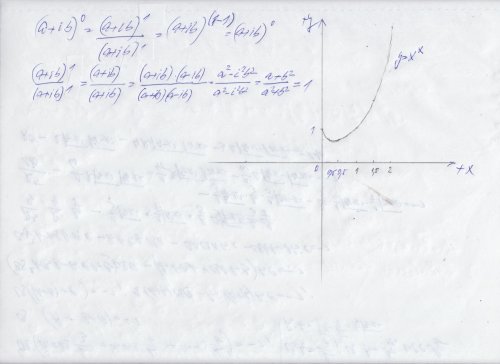
Nikoliv kromě, i nula na nultou je jedna, stačí, když si to nakreslíte, nebo určíte limitu, když x jde k nule zprava x na x tou . A pochopitelně i komplexní číslo na nultou je jedna, stačí si uvědomit, že to je vlastně z na 1 lomeno z na 1 , to je z na ( 1 - 1 ) = z na nultou a to je jedna, tak stejný výraz lomeno stejný výraz je jedna, tak můžete si to jako upravit, že vršek i spodek vynásobíte sdruženým komplexním číslem a pak po rozepsání dostanete podíl stejného součtu reálných čísel. Jinak x na x tou má lokální minimum mezi .25 na .25 a .5 na .5 a osa Y je tečnou k té křivce v tom bodě x = 0

Ahoj Pavle,

ano, a plyne to z toho, ze kazde nenulove komplexni cislo muzeme vyjadrit v exponencialnim tvaru \( z=re^{ iθ} \) pro realne \( r > 0 \) a bude platit \( z^0=r^0 e^{ iθ0} = r^0 e^0 = 1 \).

Protoze \( r, e \) jsou obe realna, muzeme aplikovat realnou analyzu. Timhle zpusobem se umocnovani komplexnich cisel dokonce zavadi, protoze lze snadno rozsirit na umocnovani komplexnim exponentem.

Co pise Milan, to pravda neni. "Nula na nultou" neni dobre definovany pojem a v pripade limitnich dukazu ve vicerozmernych prostorech je nutne ukazat, ze limita bude vzdy stejna, at uz se do nuly blizime po libovolne krivce. To ale neni potreba, dokonce i na realnych cislech muzeme snadno sestrojit funkci tvaru \( x^{ f(x)} \), ktera se bude na pravem okoli nuly blizit k libovolnemu cislu.