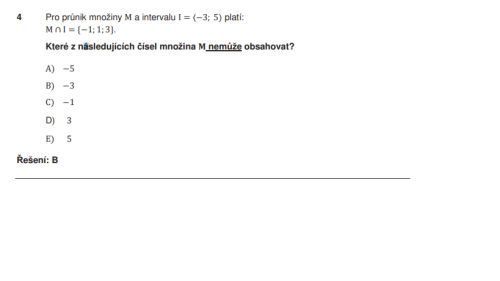
Jednoduchý příklad
Dobrý den, ráda bych poprosila o vypočítání příkladu co posílám v příloze.
Určitě se to dá jednoduše vyřešit, ale mně zrovna nenapadá jak.
Předem děkuji za odpovědi.
Pokud by jsi s tím dal někdo takovou práci, tak prosím aby mi to trošičku vysvětlil.
Denisa H.
20. 01. 2020 14:40
3 odpovědi
Pro vyřešení tohoto příkladu je nutné vědět:
a) Co je to množina bodů (množina bodu obsahuje pouze nějaké konkrétní body např 1,2,3 atd.)
b) Co je to Interval (Interval obsahuje úplně všechny cifry v něm) -To znamená, že pokud by byl interval např. od <1;2>, tak kromě čísel 1 a 2 bude obsahovat všechny čísla mezi 1 a 2 (0,5;0,51;0,6 atd.) a těch je pochopitelně nekonečno
c) Hranaté závorky a kulaté závorky intervalu - hranaté závorky nám říkájí, že to číslo tam je (takže v intervalu <1;2> tam patří i číslo 1 i číslo 2) - kulaté závorky nám říkají, že to číslo tam není (Pokud bychom měli interval <1;2), tak č. 1 tam patří a č. 2 ne, ale bude do něj patřit číslo 1,99; 1,99999999999 atd., ale ne 2)
d) Průnik - všechno to, co mají společné
řešení:
Důležité je zeptat se, co chceš zjistit. Víš, že průnik je to co mají společné. Proto hledáš cifru (odpověď), která spadá do intervalu, ale nespadá do průniku. Když by totiž číslo náleželo intervalu i množině, tak by muselo být napsané v daném průniku (zadání). Proto budeš postupovat následovně:
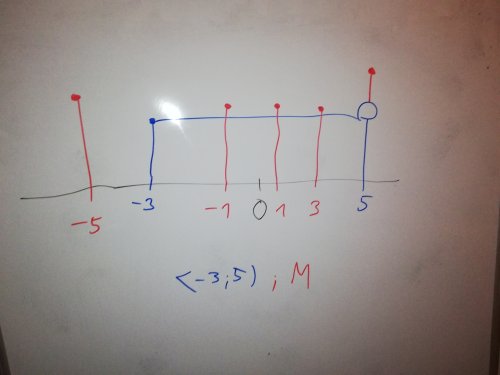
č. -5: není v intervalu (je za jeho hranicemi), ale může patřit do množiny - kdyby č. -5 bylo v intervalu muselo by být napsáno i v průniku
č. -1: je v intervalu a může být i v množině a jelikož je napsáno v průniku množiny a intervalu, tak v té množině musí být (mají to společné)
č. 3: obdobně jako č. -1
č. 5 není v intervalu, ale může být v množině (není to nijak vyloučeno)
č. -3 Je v intervalu a pokud by bylo i v množině, tak by muselo být napsané v průniku společných bodů, ale jelikož v průniku napsané není - nemůže být v množině - řešení
Zde vidíš, že body -1 1 a 3 jsou společné (průnik). Kdyby množina obsahovala č. -3, tak by se č. -3 množina (červená) muselo překrývat s č. -3 intervalu (modrá) -> muselo by tedý být napsáno v tom, co mají společné :) (ty knedlíky na koncích čar symbolizují závorky intervalu. Pokud je plný, tak tam číslo patří, pokud je prázdný viz. č. 5 v intervalu, tak tam nepatří)
K bodu b je tam chyba, myslel jsem samozřejmě 1,5 1,65 1,9999999 atd.