Koza na kruhovém dvorku

Zdravím.

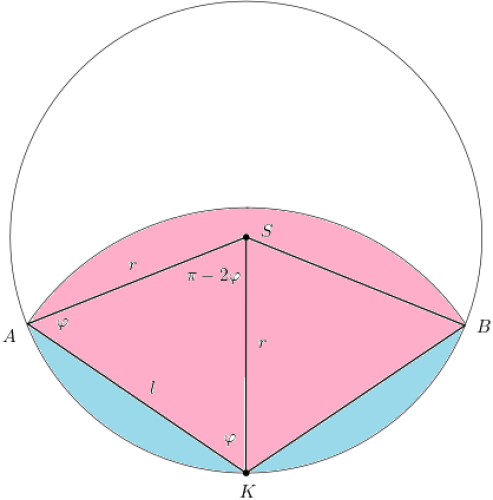
Délku provazu si označím \(l\), poloměr dvorku \(r\) a úhel \(AKS=\varphi\) (obrázek).

Trojúhelník \(AKS\) je rovnoramenný a ze sinové věty mám \(\dfrac l{ \sin(\pi-2\varphi)} =\dfrac r{ \sin\varphi} \ \Rightarrow\ l=2r\cos\varphi\) (1).

Obsah růžové kruhové výseče je \(S_1=\frac12\cdot(2\varphi)l^2=4\varphi r^2\cos^2\varphi\)

Obsah jedné modré úseče je \(\frac12r^2(\pi-2\varphi)-\frac12r^2\sin(2\varphi)\) (protože \(\sin(\pi-2\varphi)=\sin(2\varphi)\) ). Tyto úseče jsou dvě, takže

\(S_2=r^2(\pi-2\varphi-\sin(2\varphi))\)

Podle zadání má platit \(\frac12\pi r^2=S_1+S_2\), což nám dává rovnici

\(\frac\pi2=4\varphi\cos^2\varphi+\pi-2\varphi-\sin(2\varphi)\)

A nyní špatná zpráva: Tuto rovnic analyticky nejde řešit.

Pokud použiješ nějaký program na numerické řešení (použil jsem wolframalpha.com), dostaneš \(\varphi\approx 0,95\) a z (1) pak \(l\approx1,16r\)

Děkuju...paráda