Limita funkce LHospitalovo pravidlo

Vkládám jak jsem to řešila... ale nevychází to :( výsledek má být u obou příkladů 1

Máte to bez L´Hospitalova pravidla, stačí uvážit tyto limity, sin x se blíží k x, když x se blíží k nule a dále 0 na 0 = 1, což je ( lim x na x, když x se blíží k nule ) = 1 . Vyjde tedy celá limita = 1

U toho prvního, to vede vlastně na výraz ( e na ln ( 0 na 0 ) ) a to je ( 0 na 0 ) = 1

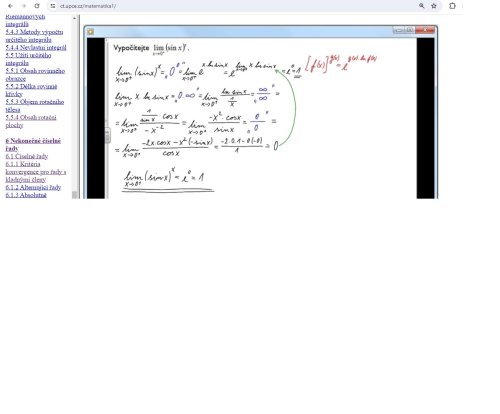
Dobrý den, děkuji za řešení. Pomocí LHospitalova pravidla jsem se totiž u toho druhého příkladu dostávala stále k derivaci sinu a kosinu a nebyl tomu konec... Ten druhý příklad řeším správně? Resp. nevím, jak dál... Děkuji moc

Tak e na ( ln x ) * ln (1+x ) ) je vlastně výraz e na ( A*B ) , kde A = ln x, B = ln ( 1 + x ) a to po úpravě určitě není jen A / B . Toho e se nejde tak zbavit, bude to ( ( e na A ) ) na B nebo i obráceně ( e na B ) na A, tedy zde ( e ln x ) na ln (1+x)

Asi jako byste napsala 8 = e na ln 8, tak e se neztratí

e se neztratilo. Řešila jsem to jako pan docent na přednášce, podle vzorového příkladu, který přikládám. Řeší to, co má u e jako samostatnou limitu a v příkladu, který přikládám se pak při výsledku nula vrátí k tomu e a e na nultou mu vyjde jedna. Snažila jsem se postupovat stejným způsobem, tedy převést to na neurčitý výraz řešitelný LHospitalovým pravidlem. Ale nula mi tam nevychází...

Asi úplně nejefektivnější je tato úvaha lim. x jde k 0 ( 1 + x ) na (1/ x je číslo e. Pak ln x = x * 1 / x * ln x a celé to rozepsat viz níže a vyjde Vám přehledně X na X když x jde k 0 = 1

Tady je také zřejmé, že nula na nultou nebere jako jedna, ale neurčitý výraz, který dále převádí na nula lomeno nulou nebo nekonečno lomeno nekonečnem stejným způsobem jako pak u druhého příkladu já - převede to na zlomky a řeší právě LHospitalovým pravidlem.

Dobrý večer, úpravy jsem už pochopila... x na x jsem si vyřešila pomocí LHospitalova pravidla tedy jako lnx lomeno (1/x) a pak to opravdu vede k e na nultou, což je jedna. Obávám se, že x na x rovnou jako jedna rovnou mi nebude uznáno, ale takto to umím "dokázat" v souladu s postupem, který je nastíněn výše. Moc děkuji za vyřešení.

$(1+x)^{ \ln x} = e^{ \ln(1+x)\ln(x)}$

Zajímá nás tedy limita

$\ln(1+x)\ln(x)$ v nule, ale to lze přepsat jako

$\frac{ \ln(1+x)} { x} x\ln(x)$

Limita prvního činitele je 1, neboť je to známá limita, ořípadně lze ukázat l'Hospitalem.

Limita druhého činitele je 0, opět známá limita, případně l'hospital na $\frac{ x} { 1/\ln(x)}$

Z limity součinu je tedy limita mocnitele nula, tj příklad vyjde e⁰=1.

Děkuji moc, už je mi to jasné.