Najděte limitu - limita vychází 0/0 a zvláštní úprava?

Zdravím,

mám následující zadání:

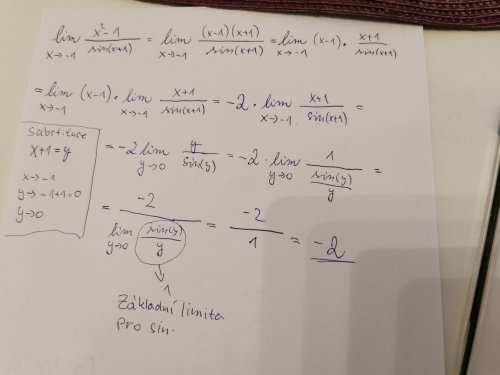
$\lim\below{ x\ \rightarrow\ -1} { \left(\frac{ x^2\ -\ 1} { \sin{ (x\ +\ 1)} } \right)^}$

Při x0 = -1 vychází ve jmenovateli 0, což nemůže a proto je potřeba nějaká úprava. Po dlouhém přemýšlení jsem nahlédl do výsledků.

Nejdříve se udělá úprava jmenovatele na (x - 1)(x +1)

Pak se stane ale něco co zcela nechápu jak k tomu lze dojít.

$(x\ -\ 1)\frac{ 1} { sin(x+1)/(x\ +1)}$

Ještě je zde vysvětlivka, že sin(y)/y -> 1; y -> 0

Co mi dovolilo udělat takovou operaci?

Děkuji.