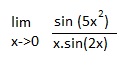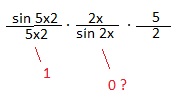Limita goniometrické funkce

Úplně snadno: stačí přemýšlet, jak se zbavit nepříjemných funklcí a jejich argumentů, sám vidíte, že se to přehledně co nepotřebujeme, vynuluje.

Zkrátka, stačí rozvést v McLaurinovu řadu, nahoře je argumentem ( 5 x ^ 2 ) , dole ( 2 x ) , pak vytknout společný prvek nahoře to je těch 5 x ^ 2 , společný prvek dole , to je těch 2 x a ten přenásobit tím osamoceným x a v závorce nahoře i dole zůstane ( 1 - cosi) / ( 1 - cosi) a před zlomkem 5 / 2 * ( x ^ 2 / x ^ 2 ) = 5 / 2 a v závorce po přímém dosazení ( nahoře i dole ) 1 - nula na cokoliv dělená čímkoliv = 1 a to samé dole, čili 1/1 = 1 a to již neovlivní těch 5 / 2, což je ta limita

Děkuji, jdu si to projít !

Stačí rozšířit zlomek, abychom z toho dostali základní limitu \( \frac{ \sin x} { x} \) a pak použít větu o součinu limit.

\( \lim_{ x \to 0} \frac{ \sin 5x^2} { x \sin 2x} = \lim_{ x \to 0} \frac{ \sin 5x^2} { 5x^2} \frac{ 2x} { \sin 2x} \frac{ 5} { 2} = \frac{ 5} { 2} \)

Díky a mohu se zeptat čím jste zlomek rozšiřoval ?

možná tímhle zlomkem

\(\frac{ 5{ x} ^{ 2} 2x} { 5{ x} ^{ 2} 2x}

\)

To snad stačí zpětně roznásobit, ne? :)

Přenásobíš původní zlomek \( \frac{ 5 . 2 . x} { 5 . 2 . x} \), nahoře použiješ \( 2x \) a dole \( 5x \), jak je vidět v obou zlomkách. Pak tam zůstane \( \frac{ 5} { 2} \).

Jasný chápu!

A můžu se ještě zeptat kolik je ten zlomek 2x / sin 2x

když dosadím 0 tak vyjde 0, a tím pádem by to celkem byla taky 0

To je právě to, co nemusíte "řešit" kdybyste to udělal jak jsem Vám napsal, kde se vše co "nepotřebujete" vynuluje. Zde musíte nejprve vědět, že když ( * ) - > 0 , pak sin ( * ) -> ( * ) , čili jinými slovy, pro malé argumenty se sinus ( * ) prakticky rovná svému argumentu, takže to není 0 / 0 , ale vlastně ( * ) / ( * ) = stejný argument / stejný stejný argument = 1, tak stačí si to namalovat v jednotkové kružnici a uvidíte proč, nebo to odvodit klasicky (jak se to jako vyučuje) a nebo takto (jak se to běžně nevyučuje) :

a navíc je mnoho takových výrazů, které rozložit či podobně upravit (jakoby klasicky) je prakticky nemožné a pak je to řešitelné jedině přes rozepsání do McLaurinovy řady

MILAN - díky! budu si muset dostudovat tu Maclaurinovu řadu

Funkce \( \sin x \) se definuje tak, aby vyšla \( \lim_{ x \to 0} \frac{ \sin x} { x} = 1 \). Proto se tenhle vztah nedá dokázat a už vůbec ne přes Taylorův rozvoj (resp. McLaurinovu řadu), protože k němu potřebujeme znát hodnotu téhle limity.

K otázce: \( \lim_{ x \to 0} \frac{ 2x} { \sin 2x} = \lim_{ x \to 0} \frac{ 1} { \frac{ \sin 2x} { 2x} } = \frac{ "1"} { "1"} = 1 \)

Btw, hodně bych se divil, kdyby ti v písemce uznali toho Taylora, tohle je jednoduchý příklad na úpravy zlomků (učivo základní školy) a znalost základní limity.

Dík už je mi to jasný

Taky myslím, že to bude jednodušší příklad /tedy alespoň pro toho, kdo to ovládá :)

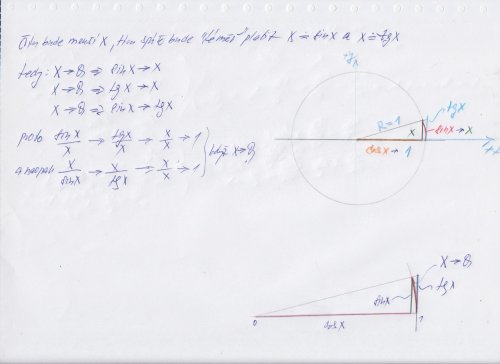
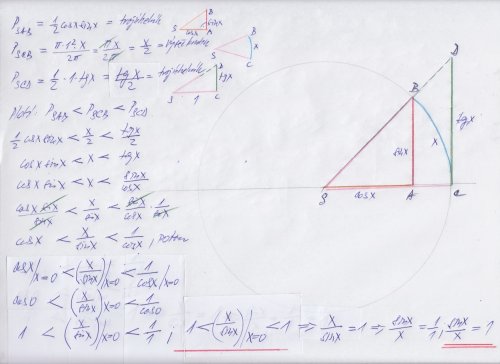
Tak jako limita ( pro x jde k nule) výrzu ( sin 2 x ) / ( 2 x ) = 1 , tak podobně ( 2 x ) / sin ( 2 x ) = 1 / 1 = 1 , prostě ten "základní" tvar sin argumentu / argument má stejnou limitu, jako argument / sinus argument , je to jen "převrácená" hodnota jedničky a to je pořád jednička . a jinak graficky :

Prostě ta poloviční tětiva, což je sinus x, se bude tím více "skoro" rovnat oblouku x, když ten oblouk x bude stále "kratší" čili se bude blížit k ose X. A pochopitelně čím je oblouk kratší, tím spíše je cosinus toho "krátkého" oblouku roven 1 a toho se využívá třeba dávno v katastrální geodesii, když se dělají oměrky polárně měřených bodů (totálkou , třeba TRIMBLE), tak se nehlídá sklon pásma a může být pro délky do 30 m třeba sklon 6° a je to pod dopustnou odchylkou pro přímo měřené kontrolní délky. Tak 30 m - 30 m * cos 6° = 16 cm a to je méně, než jednonásobek střední chyby délky md = 20 cm

Děkuji za nákres, a přeji hezký večer

Ještě jeden důkaz, proč limita ( x -> 0 ) ( sin x ) / x = 1 přes plochy trojúhelníků a výseče mezi nimi a větě o "sevření".

Jinak funkce sinus v praxi existuje a byla používána již před cca 1500 - 2200 lety, aniž v Indii (odkud název pochází) něco znali o definicích a limitách, takže ani náhodou ji nemohli definovat Indové (ani Helléni) jako aby poměr sin x / x když x jde k nule dal jedničku, na to se přišlo až o cca 1200 let později, když již dávno existovala a byla používána a v Indii ji "definovali" pokud se to dá tak vůbec nazývat, jako poměr poloviční tětivy ku poloměru a to jim stačilo, (o limitách neměli ponětí), proto jí říkali jiwa (= tětiva), pak Arabové dále přechýlili na džajb (džín - yad - báth) = dž(a)jb = (záliv = sinus). Takže Evropa ji jen převzala tak jak "byla k mání dávno" a limity se začaly používat, až když dobrých 1300 let již existovala a tak byla i nazývána. Proto nemohla být zavedena s tímto předpokladem, aby sin x / x = 1 když x jde k nule, to je jen důsledek, na funkci jako takové se nic nezměnilo za těch 1500 let. Prostě, v době, kdy se limity začaly tak nějak užívat, již "měla z sebou" 1200 - 1800 let aktivního užívání a limity se objevily až pozdě v mezičase.

To je tak mimo mísu, že fakt nepoznám, jestli jen trolíš. :)

K výše uvedenému Tomášovu řešení bych ještě dodal, že využíváme Větu o aritmetice limit a Větu o limitě složené funkce. Aby ti náhodou neubrali body.