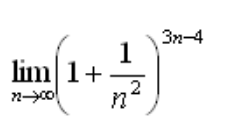Limita posloupnosti

Myslím, že bychom mohli posloupnost nahradit funkcí a použít L´Hospitalovo pravidlo. Limita je typu 1 na nekonečno, upravíme ji na tvar nula lomeno nulou. Schematicky, limita pro x jdoucí do nekonečna:

$lim A^B=e^(ln (lim A^B))=e^(lim ln(A^B))=e^(lim B ln(A))$

kde je limita typu nekonečno krát nula, kterou přepíšeme na tvar nula lomeno nulou

$lim B ln(A)=lim \frac{ ln(A)} { \frac{ 1} { B} }$

Podle Hospitalova pravidla derivujeme zvlášť čitatele a zvlášť jmenovatele, vyjde nula.

Výsledek je tedy $e^0=1$.

No, ten zápis není právě excelentní :)

V prvním řádku je číslo e umocněno na ln(lim(A^B)).

Dakujem velmi pekne, musim si nastudovat Hospitalovo pravidlo. Aspon mam way to go! :D

Jestli je to vš příklad a neměli jste Hospitalovo pravidlo, tak to jde asi ještě jinak. Mohli by to vědět tady ****

Poznámka: Odkaz odebraný moderátorem. Řešte problém, prosím, na tomto fóru.

Využiješ následující rovnosti

$(1+\frac{ 1} { n^2} )^{ 3n-4} = (1+\frac{ 1} { n^2} )^{ n^2 \frac{ 3n-4} { n^2} } = ((1+\frac{ 1} { n^2} )^{ n^2} )^\frac{ 3n-4} { n^2}$

Limita v závorce půjde k $e$ , a protože je to konečné číslo, budeš umocňovat $e$ na "nulu", takže vyjde 1.