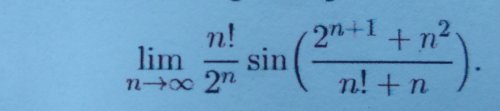Limita posloupnosti

Jediné, co mě napadá, je nějak použít větu o sevření na dolní a horní odhad toho faktoriálu a pak pomocí Heineho věty převést problém na limitu funkce a použít větu o limitě složené funkce na známou limitu sin(x)/x. Nějak mě ale nenapadají ty správné odhady.

Ahoj, kromě Heineho věty a věty o limitě složené fce je zde potřeba znát limitu podílu \( \frac{ 2^n} { n!} \) . To je od určitě chvíle bráno jako "známá věc", a je to \( 0 \), ten faktoriál roste totiž mnohem rychleji než ta exponenciála – jde to náhlednout, když si člověk rozepíše faktoriál z definice a (v našem případě) odhadne \( n! \geq 1 \cdot 2 \cdot 3 \cdot 3^{ n-3} \) . Pak to vypadá, že to, co je argumentem sinu, jde k nule a nikdy není nulou (je třeba dokázat). Dál je to snad jasné. :-)

To ano, ale jak se zbavím toho faktoriálu? Přeci nemohu tuto limitu převést jen tak pomocí Heineho věty? Žádný zobecněný faktoriál jsme si nedefinovali, takže mi tam vadí právě to, že by tam bylo něco jako x! :)

Jo takhle, no my můžeme Heineho použít až na limitu funkce \( \frac{ \sin(x)} { x} \) pro \( x \rightarrow 0 \) . Větu o limitě složené fce pak ani nepotřebujeme. :-)

Zkuste takto, ale zkontrolujte si to, může to být i jinak

Taylor mi přijde zde jednak příliš silný nástroj a jednak to moc neřeší ten problém spojité funkce vs. posloupnost. Já měl na mysli rovnou použít Heineho pro funkci \( \sin(x)/x \) a posloupnost \( x_n = \frac{ 2^{ n+1} +n^2} { n!+n} , n \in \mathbb{ N} . \) Heine se použije pro \( \lim_{ n \rightarrow \infty} \frac{ \sin(x_n)} { x_n} = 1 \). Věřím, že teď už jasné, jak jsem to myslel. :-)

Může být takto? Taylora na to nechci používat.

Pardon, nemá tam být 0 ale 1 u té standardní limity samozřejmě:)

Vše správně, jen dvě nepřesností. První již opravena :D Druhá je asi taky hned vidět, stačí ještě jednou pozorně projít. :-)

Takto? :D

To jste sice opravila správnou věc, ale na špatném místě :D \( x_n \) je jen ten argument sinu, takže naopak tam má být \( \sin(x_n)/x_n \), a to i na 4. řádku, to je ta druhá chybka :-)

Jo to je pravda :D moje chyba za špatné označení. Jinak Vám děkuji za pomoc. :)

Rádo se stalo :-)