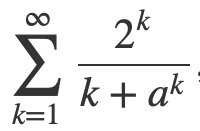Limita řady
Dobrý den, potřeboval bych pomoct s vyšetřením konvergence této číselné řady:
Adam B.
20. 10. 2020 22:10
9 odpovědí
Pro upřesnění a je reálný parametr.
Ahoj Adame, bude to konvergovat pro a>2. Odhadnes to shora geometrickou radou s kvocientem mensim nez jedna.
Jo a ted si nejsem uplne jistej, ale je mozny ze to bude konvergovat i pro a < -2.
Díky za odpověď, mohl bych ještě zeptat proč zrovna 2 ?
\( \sum_{ k=1} ^{ \infty} \frac{ 2^k} { k+a^k} < \sum_{ k=1} ^{ \infty} \frac{ 2^k} { a^k} =\sum_{ k=1} ^{ \infty} (\frac{ 2} { a} )^k \)
A tahle geometrická řada bude konvergovat když a>2, aby kvocient byl menší než 1. No a akorát by to ještě chtělo rozmyslet, co se bude dít, když a bude menší než dva. intuice mi říká, že to bude taky konvergovat, protože to k ve jmenovateli je zanedbatelný, ale chtělo by to zase nějak odhadnout.
ta geometrická řada bude konvergovat absolutně, takže toho by se mělo nějak využít. Akorát se mi teď nedaří udělat ten odhad :-).
Diky moc, konecne to chapu :D
Dobrý den, pardon, že se zase k tomu ještě vracím, myslel jsem, že už to zvládnu, ale...:D mam to vyřešené pro všechny intervaly kromě intervalu <-2, 0> a nevím co s tím. Myslím si, že tam nějak musím vyvrátit nutnou podmínku konvergence, ale nevím jak. Možná nějak vybrat dvě podposloupnosti o různých limitáach ?
Díky moc za reakci
No pro tyhle acka ta limita neexistuje, bude akternujici rada ktera navic neaplnuje nutnou podminku konvergence. Rozdel si to na sudy a lichy cleny.