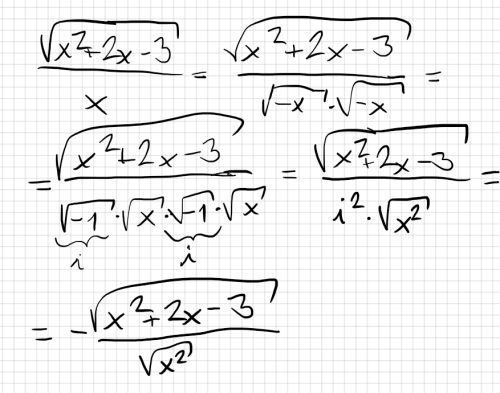Limita x->-inf arctg (x+sqrt(x^2+2x-3))
Ahoj, počítal jsem příklad: lim x->-inf arctg (x+sqrt(x^2+2x-3))
prvně co jsem udělal, je že jsem si vzal samostatně x+sqrt(x^2+2x-3) a rozšířil jsem si to "jedničkou" x-sqrt(x^2+2x-3)/x-sqrt(x^2+2x-3) po úpravách jsem se dostal (3-2x)/(x(1-(sqrt(x^2+2x-3)/x).
Po další úpravě a rozdělení jsem se dostal k tomuto (je to jen část):
lim x->-inf sqrt(x^2+2x-3)/x
a když budu chtít x dát dovnitř té odmocniny tak mi vyjde toto:
lim x->-inf -sqrt(1+2/x-3/x^2)
A má otázka je. Proč tam musím dát to "minus" před tu odmocninu. Mě napadlo to, tím že je to limita kde x jde k - nekonečnu tak do odmocniny bych neměl dát to mínus, takže jsem to dal před to... Jestli by byl někdo hodný a vysvětlil by mi to trochu více odborněji :D
Děkuji za odpověď
(výsledek je -pi/4)
Filip N.
17. 03. 2021 20:16
3 odpovědi
Jak nad tím tak přemýšlím. tak mě napadlo ještě toto
Zdravím, podíváme se jen na toho jmenovatele
\(x-\sqrt{ x^2+2x-3} =x-\sqrt{ x^2(1+\frac2x-\frac3{ x^2} )} \)
A teď přichízí ta chyba: \(\sqrt{ x^2} =|x|\)
Takže dostáváš \(x-|x|\sqrt{ 1+\frac2x-\frac3{ x^2} } \)
Stačí?
Jo, Děkuji :)