Numerické řešení rovnice
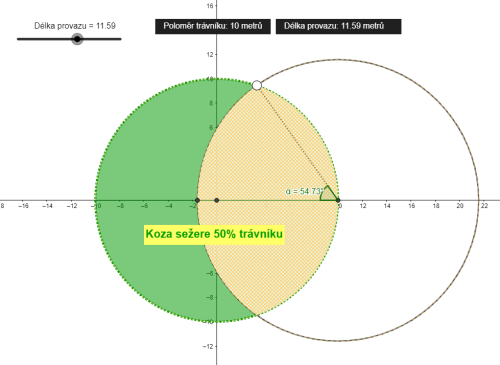
Zasekl jsem se na jedné úloze ze sbírky, úloze o koze ...přeformulováno do řeči geometrie: Mějme kružnici \(k_1\) o poloměru \(r_1\)=10, a kružnici \(k_2\) se středem ležícím na \(k_1\) takovou, že rozdělí obsah kruhu \(k_1\) na části o stejném obsahu. Jakou velikost má poloměr \(r_2\) kružnice \(k_2\) ?
Vyšlo mi (klasicky, ze vztahů délky/plochy/úhly pro úseče/výseče/trojuh.):
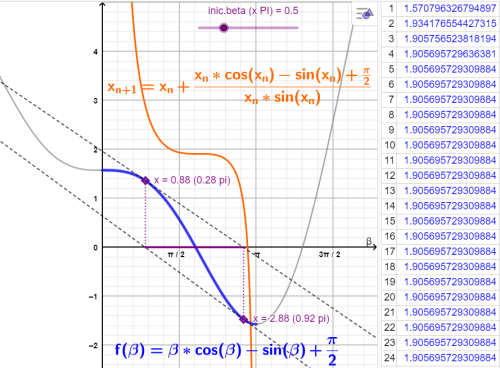
\(\beta*cos \beta - sin \beta + \frac{ \pi} { 2} = 0
\)
\(r_2 = cos \left ( \beta/2 \right ) * 2 * r_1
\)
\(\left [ \beta=2\alpha \right ]
\) ...viz obrázek
Beta se nedá přímo spočítat...
Petr F.
29. 05. 2021 21:10
4 odpovědi
Chtěl jsem položit dotaz (poradit jakou num.metodu nejvhodnější použít) a byl jsem ukončen, mea culpa ...bohužel to mrší latex, píšu to znova, snad se zadaří :)
\(\beta*cos \beta - sin \beta + \frac{ \pi} { 2} = 0
\)
\(r_2 = cos \left ( \beta/2 \right ) * 2 * r_1
\)
\(\beta = 2 \alpha \)
První funkci lze řešit nejjednodušší Newtonovou metodou půlení intervalů - z vykreslení grafu funkce nebo z vyšetření monotonosti (za předpokladu, že hledáme hodnotu mezi nulou a přímým úhlem) plyne, že je tam pouze jedna nulová hodnota a tím pádem tato metoda určitě uspěje.
Druhá rovnice pak již po dosazení \(\beta \) přímo definuje poměr velikosti poloměrů.
Logika té metody je následující:
- Vyhodnoť funkční hodnotu ve třech bodech - kraje intervalu a jeho polovina.
- Nech si ten prostřední + krajní, v němž má funkční hodnota opačné znaménko
- Použij výsledek bodu 2) jako vstupní interval bodu 1)
Iteruje se, dokud není velikost vstupního intervalu pod hranicí požadované přesnosti výpočtu.
Díky za Newtona ...na monotonním intervalu a volbou x1 x2 jako krajních bodů aby se zaručilo že kořen leží uvnitř je to univerzální metoda a předpokládám že rychlost s jakou konverguje ani nezáleží na dané funkci (po 13 krocích přesnost 3 desetinná místa).
Vyzkoušel jsem metodu aproximací funkce jako tečen v bodě (x,f(x)) kde má směrnici k=-x*sin x u funkce f(beta). Z grafu je patrné že se trochu zmenšil interval x na kterém iterace konverguje, výhodou je je minimální počet kroků k dosažení přesného výsledku.