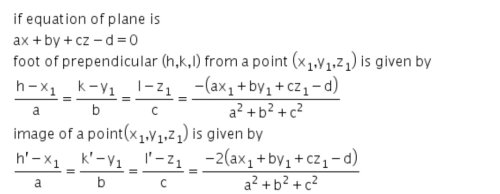Odvození rovnic zobrazení osově souměrného bodu
Krásný den. Poprosil bych někoho o důkaz/odvození těchto dvou krásných rovnic pro přímý výpočet osově souměrného bodu vůči rovině.
Obrázek je v angličtině, takže zde trocha osvětlení z pohledu jazyka:
Rovina je dána obecnou rovnicí, bod [x1; y1; z1].
Bod [h; k; l] je patou kolmice vedené bodem [x1; y1; z1], bod [h'; k'; l'] je bodem osově souměrným k bodu [x1; y1; z1].
Předem moc děkuji, nejsou to úplně běžné rovnice (už to, že využívá kanonických rovnic přímky je v Česku atypické) a rád bych věděl, jak se k ní přišlo. :)
Zdravím,
Kája
Karel T.
21. 01. 2022 09:06
2 odpovědi
Způsobů odvození je hodně, jestli máme zůstat v analytické geometrii, tak se jedná o jednoduchou optimalizační úlohu.
Hledáš bod \( (h,k,l) \), který je nejblíž bodu \( (x_1, x_2, x_3) \) a leží na množině dané rovinou. Vzdálenost měříme euklidovsky, takže Pythogorova věta. Minimalizujeme funkci s omezením, takže Lagrangeovy multiplikátory.
V příloze je ukázka první části, ta druhá už bude jen geometrie.
Ještě dodám, že když je člověk trochu zběhlý v lineární algebře, je ten vzorec poměrně intuitivní.
\( \frac{ h-x_1} { a} = -\frac{ ax_1+bx_2+cx_3-d} { a^2+b^2+c^2} \)
Zjednoduším si život a položím \( d=0 \), tím jen říkám, že rovina prochází počátkem. Pak pár jednoduchých úprav.
\( x_1-h = \frac{ ax_1+bx_2+cx_3} { a^2+b^2+c^2} a \)
A tady už je jasně vidět, o co jde, protože na pravé straně je jen vnitřní součin na euklidovském prostoru.
\( x_1-h = \frac{ \left< (a,b,c),(x_1,x_2,x_3) \right>} { |(a,b,c)|^2} a \)
Navíc máme první komponentu nějakého bodu, když to vyjádříme vektorově, dostaneme, že vzdálenost bodu \(X\) od paty kolmice \(P\) odpovídá projekci \(X\) na normálu \(V\) dané roviny.
\( X-P = \frac{ \left< V,X \right>} { |V|^2} V \)