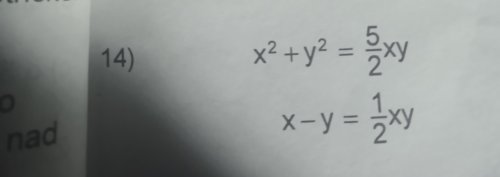Soustava kvadr. rovnic

Jednoduše viz níže :

řešením jsou dva body o souřadnicích x1,y1, a x2,y2. Můžete si to představit, jako dvě funkce o dvou proměnných, kde v horní rovnici je fLevá(x,y) se rovná fPravá(x,y). Podobně u dolní rovnice nějaká jiná gLevá(x,y) se rovná gPravá(x,y) . Z toho vzejdou společné body té funkce a jelikož je druhého řádu, musí být tedy dva. dosazením je vidět, že body řešení souhlasí. Prostě z=f(x,y) (levá) a to dá totéž jako z=f(x,y) (pravá) po dosazení souřadnic bodu A1 , A2 (které jsou vlastně tím řešením těch rovnic) a to samé pro z= g(x,y) (levá) dá z = g(x,y) (pravá) opět po dosazení A1, A2

Zdravím,

jen bych chtěl upozornit, že kolega Milan udělal v rovnici

\((x-y)^2=(x-y)\) nekorektní úpravu (zkrátil výrazem \(x-y\)), takže mu jedno řešení vypadlo.

Správný postup:

\((x-y)^2-(x-y)=0\ \Rightarrow\ (x-y)(x-y-1)=0\)

Druhou závorku vyřešil, ale ještě musíš dopočítat vyriantu \(x=y\)

Nešlo to již opravit, jinak pro x=y je vidět, že to vyhovuje bodu A3 [ x3 = 0 , y3 = 0 ] tedy počátku souřadnic . Je vidět "ihned" , že ty plochy se protínají v tomto bodě, jelikož první výraz z = x ^ 2 + y ^ 2 představuje rotační paraboloid a takto zapsán prochází počátkem souřadnic, z = x - y představuje rovinu, která také prochází počátkem souřadnic a z = k * xy představuje zborcenou přímkovou plochu, která také prochází počátkem souřadnic.