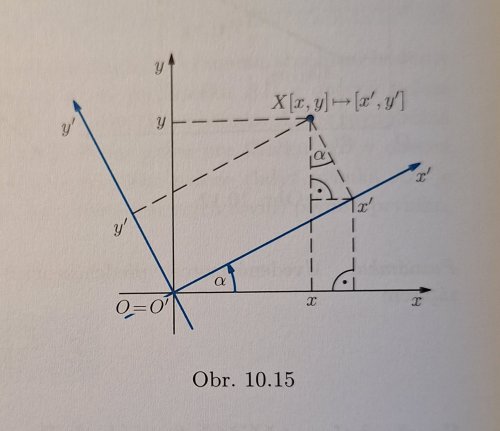Transformace pravoúhlé soustavy souřadnic otočením

Ahoj Marku,

ten obrazek je hrozne matouci, protoze x' znaci soucasne osu i bod.

Na modre ose x' je prunik s kolmici oznaceny taky jako x' a tenhle bod se rotuje o uhel alfa do bodu [x,y] v puvodni soustave. Klicove jsou ty vzorce \( x = x' cos\alpha - y' sin\alpha \) a \( y = ... \), ktere vyjadruji rotaci proti smeru hodinovych rucicek. Bod [x,y] je uz otoceny puvodni bod, ale vyjadreny v Oxy. Vzorce pro [x', y'] jsou inverzni rotace.

Polak ten vztah neodvozuje a vlastne ani moc nevysvetluje. Odvodit se da bud pres pouziti polarnich souradnic a pouziti trigonometrickych vzorcu pro soucet uhlu nebo primo pres definici sinu a cosinu na jednotkove kruznici.

Zkus googlit a najit nejake materialy, ktere vysvetluji rotaci v R^2, lepsiho materialu urcite najdes dost.

Zkuste podle této nižší geodesie (nenechte se zmást souřadnicovým systémem, v praxi se ten školní prostě neujal, je opačně i úhly jdou po hodinách) ale vyjde to nastejno

str. 32

str. 33

Moc děkuji za odpovědi.

Ještě jsem našel https://www.cuemath.com/algebra/rotation-matrix/

lt 34 . Dobře si všimněte v textu, že i v rovině je to fakticky úhel každé osy s každou osou (x , x´ , y , y´) , ale jen proto, že to je v rovině je tedy ta zvláštnost, že se oba doplňují na 90°, což v obecném prostoru již nejde a tam to budou směrové cosiny úhlu každé osy s každou (tak v triviálním případě občas také bude figurovat sinus, když to bude třeba jen otočení kolem jedné z os ) )

lt 35