Výpočet šesťbokeho ihlanu

Foto

Neviem ako sa dopracovali k hodnote r

Ahoj,

jaké těleso máš přesně na mysli - jak bude vypadat jeho povrch, z jakých obrazců se bude skládat?

Pravidelný mnohostěn s šestiúhelníkovými stěnami neexistuje. Může to být třeba nějaký "polopravidelný" mnohostěn, např. https://cs.wikipedia.org/wiki/Archim%C3%A9dovsk%C3%A9_t… .

Asi nejblíže je "fotbalový míč", tj. těleso, jehož povrch tvoří pravidelné šestiúhelníky a pětiúhelníky: https://cs.wikipedia.org/wiki/Komol%C3%BD_dvacetist%C4…

Takto by mal vyzerať jeden diel.

Takze nie je možné dosiahnuť s týchto segmentou “guľu “ ?

Niečo takéto

Domnívám se, že přesně nikoli, tj. z pravidelných 6-úhelníků.

Je otázka, jak to šikovně "ošidit", aby to vypadalo třeba takto:

https://www.cgbookcase.com/textures/white-hexagonal-tiles… asi je potřeba dostatečný počet šestiúhelníků.

Možná bude někde návod, nejspíš v angličtině ("sphere hexagon texture"). Jestli něco najdeš, dej mi prosím vědět. Taky se zkusím podívat.

Zdá se mi, že výše uvedený odkaz je spíš iluze.

Našel jsem toto: Skoro samé 6-úhelníky, mezi nimi je několik 5-úhelníků:

https://blender.stackexchange.com/questions/67334/how-to-turn-my…

https://www.alamy.com/vector-illustration-of-a…

Toto vypadá zajímavě pro polokouli, ale šestiúhelníky nejsou stejně velké:

https://discourse.mcneel.com/t/problems-with-hexagon…

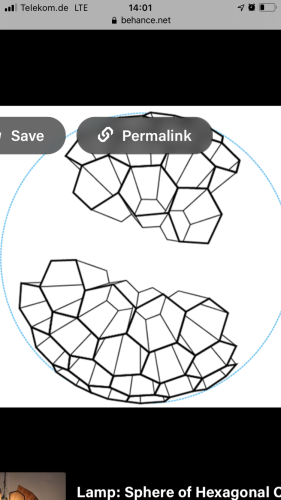
https://www.behance.net/gallery/17123817/Lamp-Sphere…

Ja som si povodne myslel že tie prázdne miesta sú zámer ale je možné z s tým iba kompenzovala to že to nevychádza ..

Nádhera... Nevyšlo by to, ale zdá se mi, že některé jehlany by ještě šly doplnit. Tak je to možná i záměr (třeba jsou pěkně vidět ty malé šestiúhelníky uvnitř).

Mám-li poradit s výpočtem, potřeboval bych vědět, které rozměry (či úhel) známe a co je potřeba vypočítat.

Áno aj takto je to super len som nechcel úplne kopírovať autora tak som chcel plnú guľu

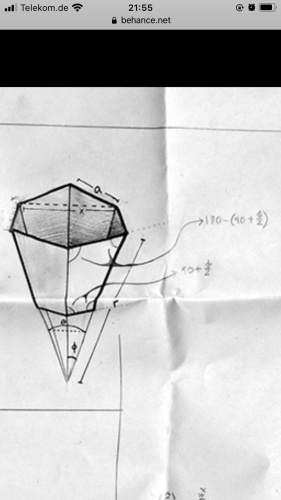
No ak som to správne pochopil tak počet segmentou si určíme sám npr 180stupnou deleno 12 je 15 taktiež stranu a npr 1.5 ako je to v tomto prepočte nie je mi jasne ako sa dopracovali k rozmeru (r) ktori použili v ďalšom prepočte

Ďalej keď dosadím (r ) do tohoroční vzorca nikdy mi nevide výsledok ako na obrázku

Je 2r myslene ako 2 x r ? Npr takto

Takto nejako my to vyšlo prvý krát keď som to prepočítal bez vzorcov na kalkulačke asi za 15 min :) :)

V podstate sa mi nejedna o nejaký konkrétny rozmer skôr o vzorce do ktorých by sa dali dosadiť hodnoty npr keď sa rozhodnem že chcem “guľu “ o priemere 40 cm ktorá sa bude skladať z velkeho počtu malých segmentou povedzme strana (a) 2cm alebo naopak z menšieho počtu veľkých segmentou npr strana 7-10cm

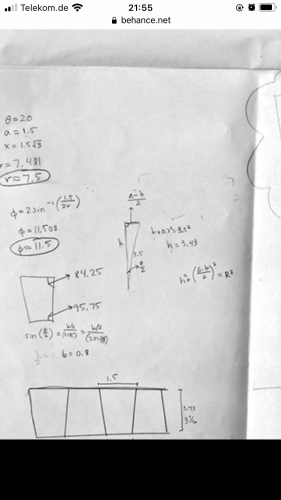
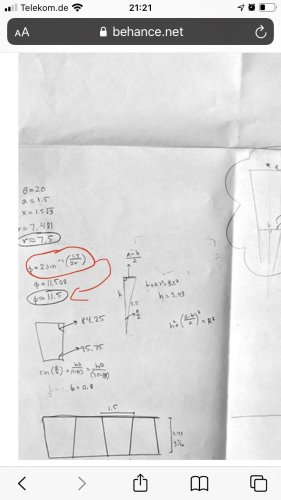
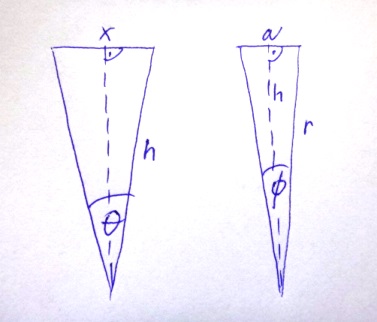
Na obrázku vpravo je boční stěna jehlanu, tj. rovnoramenný trojúhelník s podstavou \( a \), výškou k podstavě \( h \), ramenem \( r \), ramena svírají úhel \( \phi\).

Na obrázku vlevo je řez jehlanem, který je veden výškami dvou protějších stěn. Je to rovnoramenný trojúhelník se základnou \( x \) a ramenem \( h \). Úhel \( \theta \), který svírají ramena, je úhel, který svírají protější stěny.

Chceme-li mít na obvodu "koule" \( n\) jehlanů, je \( \displaystyle\theta =\frac{ 360} { n} \).

Levý trojúhelník rozdělíme na dva pravoúhlé trojúhelníky, platí

\(\displaystyle\quad\sin\frac{ \theta} { 2} =\frac{ x} { 2h} \),

odkud vypočítáme \( h \) (nahradíme \( x=\sqrt{ 3} a \)).

Podle pravého obrázku (tan znamená tangens)

\(\displaystyle\quad\tan\frac{ \phi} { 2} =\frac{ a} { 2h} \)

odtud získáme úhel

\(\displaystyle\quad\phi=2\tan^{ -1} \left(\frac{ a} { 2h} \right)\).

Dále

\(\displaystyle\quad\sin\frac{ \phi} { 2} =\frac{ a} { 2r} \),

odkud

\(\displaystyle\quad r=\frac{ a} { 2\sin\frac{ \phi} { 2} } \).

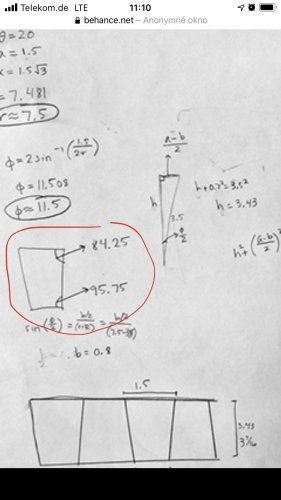
Např. pro \( \theta=20^\circ, a=1.5 \) vychází \( h=7.48086 \), \(\phi=11.450^\circ \), \( r=7.51837 \).

Super ďakujem skúsim vyrobiť pár kusov na skúšku ako to sedí a pošlem foto. Prajem pekný víkend .. ;)

Možno hlúpa otázka ale ko ste vypočítal to (h)

Z rovnice

\(\displaystyle \sin\frac{ \theta} { 2} =\frac{ x} { 2h} \)

máme

\(\displaystyle h=\frac{ x} { 2\sin\frac{ \theta} { 2} } =\frac{ \sqrt3 a} { 2\sin\frac{ \theta} { 2} } =\frac{ \sqrt3\cdot 1.5} { 2\cdot\sin10^\circ} =\frac{ 2.5981} { 2\cdot 0.17365} \)

Ale problém vidím v tom, že takto vypočítáme jen jednu řadu jehlanů kolem dokola.

Myslím si, že není nijak zaručeno, že k nim půjdou přesně připojit další tak, aby se podařilo sestavit podstatnou část "koule", možná to nepůjde vůbec.

Zdá se, že jediné schůdné řešení je na tomto obrázku, přičemž vznikne i několik pětihranů: https://www.alamy.com/vector-illustration-of-a…

Ještě se dívám na foto lampy, a připadá mi, že autor možná použil právě toto uspořádání, přičemž část jehlanů vynechal.

Domnievam sa že pripojenie ďalšej rady by malo zaruči správne nastavenie týchto uhlov .

Skúsim spraviť model a uvidíme

To riešenie s päť uholnikmy je tiež fajn myslím že mnoho ľudí to ani nepostrehne ..

Spravil som taký maly papierový model a vyzerá to dobre trochu sa tam treba pohrať z pomerom počtu segmentou a strany (a) aby segment nebol príliš krátky ale ale ok ťažko povedať má koľko je ten model presný ale to sa ukáže ak keď sa dostanem do dielne …

1

2

Zdravím, podrobnosti o těchto tělesech se mi bohužel nepovedlo najít.

Tedy jen můj názor: Myslím si, že počet pravidelných 6-úhelníků na povrchu či v jedné řadě po obvodu nelze libovolně zvolit, nejspíš se dají realizovat jen určitá (přesně vypočtená) řešení, např. snad toto https://www.alamy.com/vector-illustration-of-a… přičemž k pokrytí jsou vždy potřeba ještě 5-úhelníky, popř. jiné obrazce. Netuším, zda existuje řešení, kdy leží po samé 6-úhelníky "po obvodu".

Třeba se někomu podaří dohledat něco jistějšího. Je to zajímavý problém.

Zdravim. Je to každopádne zaujímavé. Ja som tiež hľadal ale angličtina nie je moja silná stránka. Hovorím nemecky ale v nemčine toho nie je toľko

Budem to musieť skúsiť metódou pokus/omyl. Ale každopádne bez tých päť uholnikou to určite nepojde . môže fungovať ešte to že drevo je trochu ohybný materiál a bude sa to dať trochu korigovať .Prečo sa domnievate že počet segmentov nie je možné určiť ľubovoľne..

Na různých webech nacházím řešení, která vypadají stejně. Pro menší počet jehlanů existuje řešení, kdy některé 6-úhelníky jsou nepravidelné.* Nakonec jsem si zkusil jednu možnost vypočítat a nevychází to vůbec. Ale mohu se mýlit a obecně netuším, jak na to.

• Diplomová práce: Diskrétní reprezentace ploch volného

tvaru v architektonické geometrii (na webu)

Jsem zde hostem, třeba se k tomu vyjádří někdo ze zdejších matematiků...

Přišla mi odpověď od matematika - tak předávám:

Jediné těleso, které se skládá z pravidelných 6-úhelníků (a 5-úhelníků), je toto: https://cs.wikipedia.org/wiki/Komol%C3%BD_dvacetist%C4… tj. vlastně fotbalový míč.

Všechna jiná podobná tělesa mají (bohužel) většinu 6-úhelníků nepravidelných.

Obrázek https://www.alamy.com/vector-illustration-of-a… je tedy optický klam. Proto se nám nepodařilo najít žádné matematické pojednání :)

Nakolik by se mohlo něco podařit mírnou deformací 6-úhelníků, opravdu netuším.

Ja som bol cez vykend v dielni a narezal som asi 800 dielov :) ma tie segmenty

Takze som celkom zvedavý čo s toho vide asi niečo na spôsob toho čo spravila autorka toho svietidla na fotke (pošlem foto )

Každopádne ďakujem načerpal som veľa inšpirácie a spoň mi je jasne čo je možné .