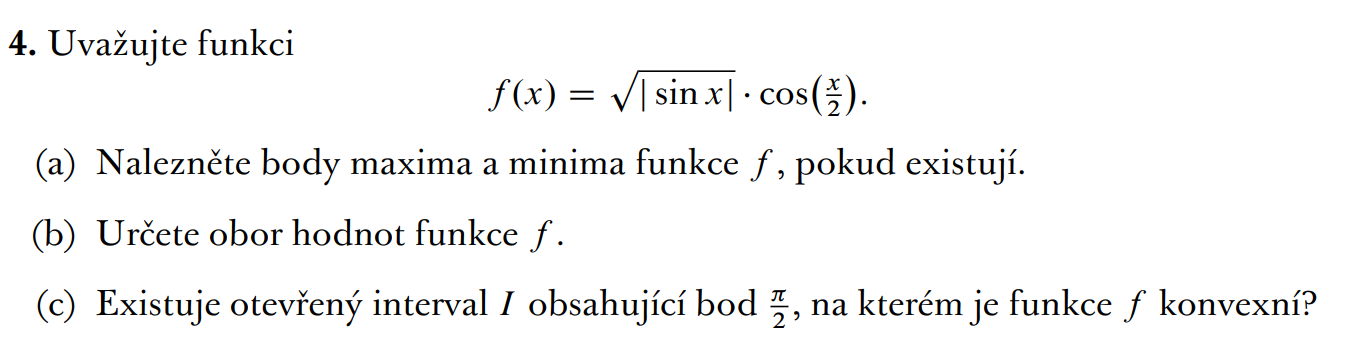Extrémy funkce

$f(x) = \sqrt{ \left|\sin(x)\right|} \cdot\cos(\frac{ x} { 2} )$

funkce je $4\pi$ periodicka, nabyva kladnych i zapornych hodnot, nulove body v $k\pi$

spocitame derivaci na intervalu $(0, \pi)$,

$f'(x) = \frac{ 1} { 2} \left[\frac{ \cos(x)\cdot\cos(\frac{ x} { 2} )} { \sqrt{ \sin(x)} } - \sqrt{ \sin(x)} \cdot\sin(\frac{ x} { 2} )\right]$

$f'(x) = 0$

$\Rightarrow \frac{ \cos(x)\cos(x/2) - \sin(x)\sin(x/2)} { \sqrt{ sin(x)} } = 0$

$\Rightarrow \cos(x)\cos(x/2) - \sin(x)\sin(x/2) = 0 \land x != k\pi$

$\Rightarrow \cos(\frac{ 3x} { 2} ) = 0 \land x != k\pi$

$\Rightarrow \frac{ 3x} { 2} = \frac{ \pi} { 2} + k\pi \land x != k\pi$

$\Rightarrow x = \frac{ \pi} { 3} + \frac{ 2k} { 3} \pi \land x != k\pi$

Pozor, jen na intervalu $0..\pi$

Je potreba spocitat i pro interval $\pi..2\pi$

Z abs hodnoty dostaneme -, to vyleze nekde v derivacich, ale na nulove body to vliv mit nebude

Vidime, ze reseni jsou:

$\frac{ \pi } { 3}$ : max,

$\frac{ 5\pi } { 3}$ : min,

$\frac{ 7\pi } { 3}$ : min,

$\frac{ 11\pi } { 3}$ : max

Plus perioda $4\pi$ (z kresleni)

Obor hodnot dostaneme jako interval mezi minimem a maximem:

$f\left(\frac{ \pi} { 3} \right) = \sqrt{ \frac{ \sqrt{ 3} } { 2} } \frac{ \sqrt{ 3} } { 2}$

$f\left(\frac{ 5\pi} { 3} \right) = -\sqrt{ \frac{ \sqrt{ 3} } { 2} } \frac{ \sqrt{ 3} } { 2}$

$H(f) = \left[-\sqrt{ \frac{ \sqrt{ 3} } { 2} } \frac{ \sqrt{ 3} } { 2} ,\sqrt{ \frac{ \sqrt{ 3} } { 2} } \frac{ \sqrt{ 3} } { 2} \right]$

Vypocteme druhou derivaci:

$f'(x) = \frac{ \cos\left(\frac{ 3x} { 2} \right)} { \sqrt(\sin(x))}$

$f"(x) = \frac{ -\sin\left(\frac{ 3x} { 2} \right)\frac{ 3} { 2} \sqrt{ \sin(x)} - \cos\left(\frac{ 3x} { 2} \right)\frac{ 1} { 2\sqrt{ \sin(x)} } } { \sin(x)}$

Zkusime dosadit $x = \frac{ \pi} { 2}$

$f"\left(\frac{ \pi} { 2} \right) = \frac{ -\frac{ \sqrt{ 2} } { 2} \frac{ 3} { 2} + \frac{ \sqrt{ 2} } { 2} \frac{ 1} { 2} } { 1} = -\frac{ \sqrt{ 2} } { 2}$

Druha derivace je v tomhle bode zaporna, tedy funkce je konkavni, tedy nemuzeme najit interval s timto bodem, kde by byla konvexni.