Kocka a dve pohybujúce sa body

Špatná otázka, otázka by neměla znít v jakém bodě, ale v jakém okamžiku. Ospravedlnuji se za chybu.

Ahoj Otto, je to nádherná úloha. Natočím na to videjko, už si ho připravuju. Marek

Ahoj,

jestli jste se učili derivovat, postupoval bych takto:

Zvolím soustavu souřadnic s počátkem v bodě A, osu $x$ ve směru AB, osu $y$ ve směru AD, osu $z$ ve směru AE.

Obě úsečky zapíšu parametricky (parametrem bude čas). Hranu krychle označím $a$. Na začátku je $t=0$, na konci $t=1$.

Ze zadání je patrné, že oba pohybující se body přejdou z jednoho krajního bodu úsečky do druhého za stejnou dobu (např. budou ve stejnou dobu v polovině úseček).

Můžu tedy v každém okamžiku určit jejich vzdálenost $d$ (dále pro zjednodušení zvolím $a=1$). Dostanu funkci, kde vzdálenost $d$ závisí na času $t$. Funkci derivuji a derivaci položím rovnu nule (hledám extrém). Z této rovnice vypočítám čas $t$, kdy jsou body nejblíže.

Jojo, přesně takhle bych na to šel, ale vzhledem k tomu, že to Otto dal do kategorie střední škola, tak nevím,jestli můžeme používat derivace (někde se to probírá na SŠ, někde ne). Každopádně ta funkce, která popisuje vzdálenost je odmocnina z kvadratické funkce a její minimum se dá najít i bez derivace.

Ahoj Otto.

To, co ti radí předřečníci bude jistě fungovat, ale není nutné problém řešit v prostoru.

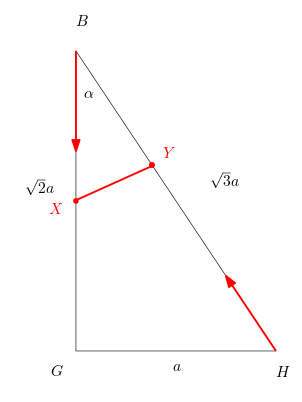
Budu předpokládat, že krychle má délku hrany $a$. Když si nakreslíš trojúhelník $\mathsf{ BGH}$ (obrázek), tak $|\mathsf{ BX} |=\sqrt2t$, $|\mathsf{ BY} |=\sqrt3a-\sqrt3t$ a $\cos\alpha=\sqrt{ \frac23}$. Označíš $|\mathsf{ XY} |=d$.

Podle kosinové věty platí:

$d^2=(\sqrt2t)^2+(\sqrt3a-\sqrt3t)^2-2\sqrt2t(\sqrt3a-\sqrt3t)\cdot\sqrt{ \frac23} =9t^2-10at+3a^2$

$=9(t^2-\frac{ 10} 9at+\frac{ 25} { 81} a^2-\frac{ 25} { 81} a^2+\frac13a^2)=9[(t-\frac59a)^2+\frac2{ 81} a^2]$

Takže nejmenší vzdálenost bude $d_{ min} =\frac{ \sqrt2} 3a$ v čase $t=\frac59a$.