Steroemetrie - koule

Zdravím,

celé ti to počítat nebudu, ale příklad 141 vypadá zajímavě.

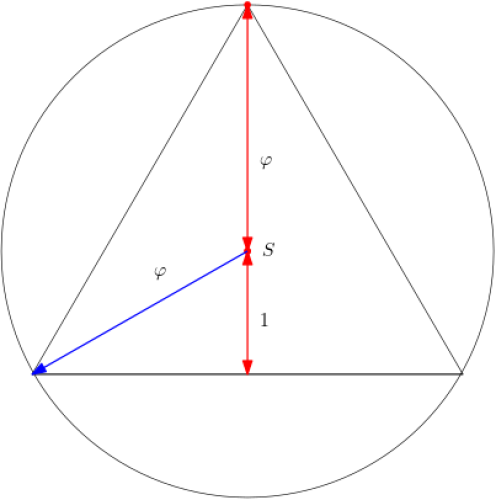
Jestli jsem zadání pochopil správně, tak (obrázek) máme poloměr koule $R=\varphi$ (a $\varphi=\frac{ \sqrt5+1} 2$). Pak objem koule $V_1=\frac43\pi\varphi^3$

Poloměr kužele $r$ určíme z Pythagorovy věty $\varphi^2=r^2+1\ \Rightarrow\ r^2=\varphi^2-1$ . Dostáváme tak objem kužele $V_2=\frac12\pi r^2h=\frac13\pi(\varphi^2-1)(\varphi+1)$

A nyní přijde kouzlo: Protože pro zlatý řez platí rovnice $\varphi^2-\varphi-1=0$, můžeme jednak psát $\varphi^2-1=\varphi$ a také $\varphi^2=\varphi+1$.

Když toto dosadíme do vztahu pro objem kužele, dostaneme $V_2=\frac13\pi\varphi^3$

Takže $\frac{ V_1} { V_2} =4$

Také mě zaujala úloha 141, uvedu jen trochu odlišný zápis. Poloměr koule označme $R$, poloměr a výšku kužele $r$, $h$, vzdálenost středu koule od středu podstavy kužele $x$.

Podle definice vznikne zlatý řez rozdělením úsečky (výšky kužele) na dvě části tak, že poměr větší části k menší je stejný jako poměr celé úsečky k větší části:

$\frac{ R} { x} = \frac{ h} { R} =\varphi$,

z toho

$x=\frac{ R} { \varphi} , \quad h=R\varphi$.

Z pravoúhlého trojúhelníku (na obrázku modrá, červená a černá úsečka)

$R^2=r^2+x^2$

a po dosazení za $x$ vyjádříme $r^2$. Do vzorce pro obsah kužele dosadíme $r^2$, $h$, nakonec vydělíme objem koule a objem kužele.

Zlatý řez: https://cs.wikipedia.org/wiki/Zlat%C3%BD_%C5%99ez

Příklad 143 je z poloviny fyzika.

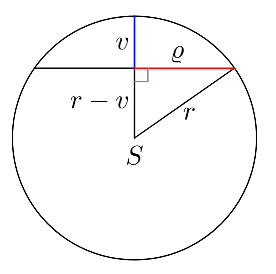
Výška kulové úseče, která vyčnívá z vody, je $v=\frac{ 2} { 5} d=\frac{ 4} { 5} r$. Objem této úseče je $V_{ nad} =\frac{ 1} { 3} \pi v^2(3r-v)$, dosadíme za $v$. Objem ponořené části $V_{ pod} =V-V_{ nad} =\frac{ 4} { 3} \pi r^3-V_{ nad}$.

Na kouli působí tíhová síla $F_G$ a vztlaková síla $F_{ vz}$. Tíhová síla $F_G=mg=V\varrho_d g$, kde $\varrho_d$ je hustota dřeva.

Vztlaková síla je podle Archimedova zákona $F_{ vz} = V_{ pod} \varrho_v g$, kde $\varrho_v$ je hustota vody.

Koule plave na hladině, obě síly jsou v rovnováze: $F_G = F_{ vz}$. Dosadíme a vyjádříme hustotu dřeva. Jestli dobře počítám, vychází $\varrho_d= \frac{ 81} { 125} \varrho_v$, což odpovídá hustotě dřeva okolo 650 kg/m3.

Ahoj, přihodím taky pár hintů....

$V = \frac{ 4} { 3} \pi \left[\left(\frac{ d} { 2} \right)^3 - \left(\frac{ d-2t} { 2} \right)^3\right]$

$\frac{ m} { \varrho} = V$

Když si to představíme, zůstane nám kulová úseč, která má v příčném řezu středový úhel $180^{ \circ} - 2\cdot 30^{ \circ} = 120^{ \circ}$

Pak už stačí dopočítat potřebné rozměry pomocí goniometrických funkcí a Pythagorovy věty a dosadit do vzorců zde: https://cs.wikipedia.org/wiki/Kulov%C3%A1_%C3%BAse%C4%8D

Opět se jedná o úlohu na kulovou úseč. Další hint bude, že hraniční body, které v příčném řezu vidíme, jsou body dotyku tečen ke kružnici a tudíž je u nich pravý úhel. Z daného trojúhelníku snadno dopočítáme potřebné rozměry a pak již odkaz viz výše.

Počítáme poměr plochy celé koule a té kulové úseče (bez podstavy)

Úloha odpovídá úloze 144, jen jsme prohodili parametry a neznámé.

Máme průnik dvou shodných koulí, jejichž středy jsou od sebe vzdáleny R. I toto je řešeno na odkaze výše.

Vzorec viz https://cs.wikipedia.org/wiki/Kulov%C3%A1_v%C3%BDse%C4…, v anglické verzi je i odvození pomocí integrálu.

Lze snadno pomocí goniometrických funkcí převést na úlohu 147.

Viz úlohy 144 a 145

Pro kulovou (i kruhovou) úseč se často hodí vyznačit si pravoúhlý trojúhelník a použít Pythagorovu větu

$r^2=(r-v)^2+\varrho^2$