Moment setrvačnosti
Dobrý den, měl bych tu tento příklad. Nevím si moc rady jak můžu vypočítat hlavní centrální momenty setrvačnosti Imin, Imax daného plošného obrazce a gyrační poloměry imin, imax elipsy setrvačnosti a její pootočení φ. Zkoušel jsem pár vzorců z tabulek, ale nepomohlo. Budu moc rád za pomoc.
zadané hodnoty:
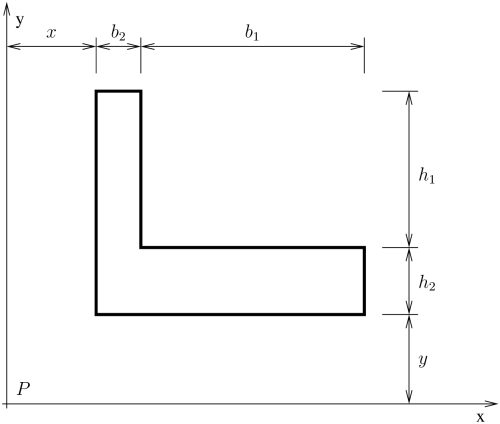
b1=9 [m]
b2=1 [m]
h1=4 [m]
h2=1 [m]
x=2 [m]
y=5 [m]
Jan N.
27. 05. 2024 15:52
1 odpověď
Vložíte do obrazce osu X, Y ( máte ji dánu předem ) . Ty dílčí obrazce jsou pravoúhlé, takže snadno spočtete momenty setrvačnosti k dílčích ploch k osám. Takže je to tvar profilu L, takže nejprve pro svislý obdélník, pak pro vodorovný obdélník a celkový moment setrvačnosti je pak vzdálenost k těžištní ose dílčího ( svislého ) * plocha ( svislého ) + vzdálenost k těžištní ose vodorovného * plocha vodorovného a tento součet vydělíte celkovou plochou a máte vzdálenost osy, kterou prochází těžiště, udělá se to pro obě osy X, Y a máte souřadnice těžiště. Skoro praktičtější by bylo vložit X do dolní podstavy vodorovného obdélníku a Y do levé hrany svislého obdélníku. To gyrační znamená setrvačnostní ( tak gyroskop je setrvačník ) . Pak poloměr setrvačnosti k ose Y je odm ( Iy / plocha ), podobně odm. ( I x / plocha ) , k počátku souřadnicové soustavy odm ( I nula / plocha ). I nula je odm ( Ix ^ 2 + Iy ^2 ) , dále spočíst deviační momenty ( pokud vzniknou ) a úhel stočení poloos elipsy ( u kružnice není co počítat, kružnice "nejde natočit" je pořád stejná ) je tg 2 D = 2DXY / ( Ix- Iy) . Ale pokud by to byl jen obdélník či jiný pravoúhlý útvar a shodně orientovaný s osami X,Y tak bude úhel stočení nula, čili osy elipsy rovnoběžné s X , Y .
Udělejte to podle tohoto :