Výpočet zrychlení z grafu
Zdravím,
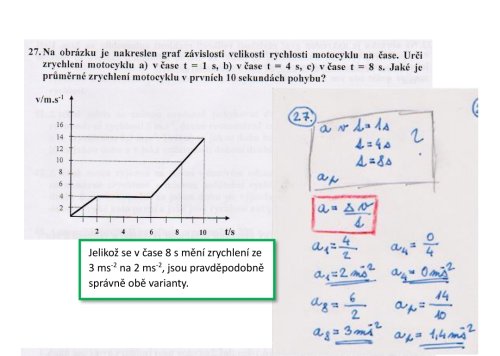
mám tady údajné řešení příkladu, ale pořád mi nejde do hlavy, proč když počítáme zrychlení v čase 1s, proč do vzorce dosazujeme 4/2 když čas má být 1.
Jaká je ta druhá metoda výpočtu průměrného zrychlení? něco jako a=∆v1 + ∆v2 ... / ∆t1 + ∆t2 ... nebo se mýlím a je pouze ta metoda a=14/10?
Předem děkuji
Adam N.
15. 11. 2023 18:21
2 odpovědi
Ahoj,
do vzorce se nedosazuje aktuální čas \( t \), ale časový interval \( \Delta t \), za který se rychlost změnila o \( \Delta v \).
zrychlení = (změna rychlosti) : (časový interval)
\(\displaystyle a=\frac{ \Delta v} { \Delta t} \)
A protože v době od 0 do 2 sekund rychlost rostla lineárně (rovnoměrně), můžeme dosadit tento interval.
Během prvních dvou sekund, tedy \(\Delta t=2\phantom{ .} \rm{ s} \), se rychlost zvýšila z 0 na 4 m/s, tedy změna rychlosti je \(\Delta v=4\phantom{ .} \rm{ m\cdot s^{ -1} } \). Dosadíme
\(\displaystyle a=\frac{ \Delta v} { \Delta t} =\frac{ 4\phantom{ .} \rm{ m\cdot s^{ -1} } } { 2\phantom{ .} \rm{ s} } =2\phantom{ .} \rm{ m\cdot s^{ -2} } \)
Ale můžeme dosadit také interval 0 až 1 sekunda nebo 1 až 2 sekundy, pak \(\Delta t=1\phantom{ .} \rm{ s} \), rychlost se za 1 sekundu zvýší o 2 m/s - a máme hned výsledek, protože zrychlení je číselně rovno změně rychlosti za 1 sekundu. Nebo dosazením
\(\displaystyle a=\frac{ \Delta v} { \Delta t} =\frac{ 2\phantom{ .} \rm{ m\cdot s^{ -1} } } { 1\phantom{ .} \rm{ s} } =2\phantom{ .} \rm{ m\cdot s^{ -2} } \)
Jak je to s průměrným zrychlením - můžeš použít "vzoreček", který uvádíš, ale to je stejné, jako vzít (celkovou změnu rychlosti) a (celkovou dobu) a vydělit je - což je jednodušší.
Z grafu je vidět, že za častový interval \( \Delta t \) = 10 s se rychlost změnila o \( \Delta v \) = 14 m/s. Průměrné zrychlení je
\(\displaystyle a=\frac{ \Delta v} { \Delta t} =\frac{ 14} { 10} \)
(v příslušných jednotkách)
To je stejné, jako když počítáme
\(\displaystyle a=\frac{ \Delta v_1+\Delta v_2+\Delta v_3} { \Delta t_1+\Delta t_2+\Delta t_3} =\frac{ 4+0+10} { 2+4+4} =\frac{ 14} { 10} \)
(v příslušných jednotkách)