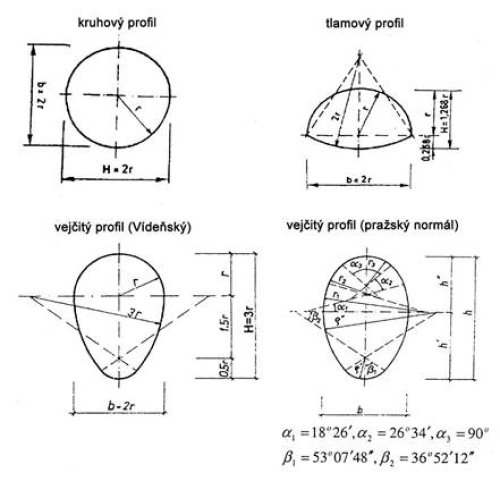
Objem vejčitého tvaru
Ahoj, potřebuji poradit se správným vzorcem pro výpočet objemu :-D
Potřebuji spočítat objem kanalizace vejčitého tvaru (Vídeňský typ), kde výška je 0,750 m a šířka 0,5 m, délka 50 m.
Vím že hydraulický poloměr R je 0,25 m. Prostě nevím, do jakého vzorečku to doplnit. Jsem na tohle tupá a potřebuji to do práce :-D
Přikládám i obrázek toho vejčitého profilu.
Zuzana G.
14. 12. 2023 09:42
2 odpovědi
Dobrý den,
budeme-li věřit údajům na stránce
http://hgf10.vsb.cz/546/VHZ2/8_podminky_navrhovani…
pro průřez vídeňské kanalizace platí vzorec \( S=4.5941 r^2\), kde \( r \) je polovina šířky, tj. \( r=b/2=0.25 { \rm m} \) a vychází \( S=0.2871 { \rm m} ^2 \).
Objem = průřez x délka kanalizace, tj.
\( V=S\cdot l=(0.2871 { \rm m} ^2)\cdot (50 { \rm m} ) =14.35 { \rm m} ^3 \).
Takže ten obvod se zřejmě skládá z několika kruhových oblouků o různých poloměrech které na sebe navazují na společných tečnách a délka těch dílčích oblouků je naznačena středovými úhly pro každý sektor. Takže vypočíst plochu "vejce" exaktně znamená nejlépe ty naznačené polární souřadnice, kterým přísluší úhly mezi poloměry jednotlivých kružnic, kde poloměry jsou vyznačeny jako poměrná část z nějakého základního "jednotkového" např. pro přehlednost převést na pravoúhlé, nebo ponechat v polárních, řešit jen polovinu podle svislé osy a sečíst plochu po sektorech mezi příslušnými body dotyku příslušných kružnic, což je sice trochu pracné, ale jde to, ten vzorečk je jinak zřejmě jen empirický, který nahražuje složitější exaktní vztah, který vyjadřuje součet dílčích ploch sektorů pro jednotlivé poloměry.