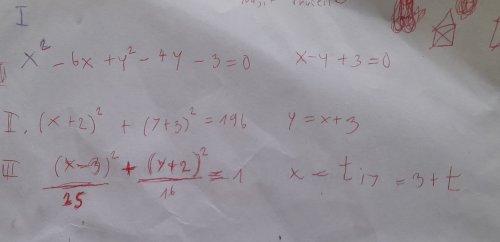Uměl by to někdo vyřešit?

Ahoj,

1. příklad

se dá řešit dvěma způsoby:

a) Z rovnice přímky

$x-y+3=0$

vyjádříme např. $y=x+3$ a dosadíme do první rovnice, což je rovnice kružnice. Dostaneme kvadratickou rovnici, která má dvě řešení $x_1, x_2$.

Pak z rovnice přímky dopočítáme $y_1,y_2$. Dostaneme dva průsečíky přímky s kružnicí $[x_1,y_1], [x_2,y_2]$.

Výsledek: $[-1,2], [3,6]$.

Obrázek pro představu: https://www.wolframalpha.com/input?i=x%5E2-6x%2By%5E2-4y-3…

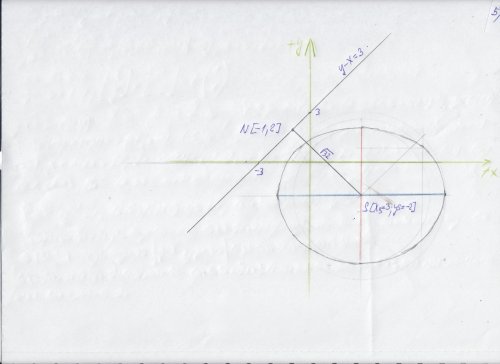
b) Rovnici kružnice upravíme na středový tvar $(x-x_0)^2+(y-y_0 )^2=r^2$. Vyjde

$(x-3)^2+(y-2 )^2=16$

tj. kružnice má střed v bodě $[3, 2]$ a poloměr $4$. Spolu s přímkou ji narýsujeme v soustavě souřadnic a zjistíme průsečíky.

Viz níže, také můžeme nejprve zkusit, zda je přímka natolik blízko středu kružnice, aby nějaké společné body byly, takže když méně než poloměr, má dva průsečíky, když stejně jako poloměr, bod dotyku, když více než poloměr, neprotínají se - str. 2, ostatní str. 1

k tomu str. 2 ( vzdálenost přímky od středu kružnice a porovnání s poloměrem )

K tomu dalšímu

Obrázek k tomu:

K té 3 )

K té 3 ) výpočet