Popis a rozbor v geometrii

První úloha je postavena na tom, že dokážeme tyto dva úhly zkonstruovat bez úhloměru. Konkrétně dokážeme zkonstruovat jejich dvojnásobky a umíme půlit úhel.

90st. sestrojíme pomocí trojúhelníku s ryskou. 60st. je vnitřní úhel rovnostranného trojúhelníku. U bodu, kde má tento úhel být tedy sestrojíme libovolně velký rovnostranný trojúhelník (pomocí kružítka).

Pomocí kružítka pak úhel rozpůlíme a dostaneme požadované hodnoty.

Ve druhé úloze využijeme vlastnost těžiště - těžiště je průsečík težnic a dělí je v poměru 2:1, kde delší část je u vrcholu, kratší u strany.

Sestrojíme tedy zadanou stranu b a potom pomocí kružítka těžiště. Pak dorýsujeme těžnice, což nám dá dostatek bodů pro dokreslení trojúhelníku.

Moc děkuji. Druhý příklad už jsem zvládla. V prvním nevím, jak dělat uhel 45stupnu, když neleží na zadané straně.

Jsou dvě možnosti.

1. Narýsovat ho kdekoliv na té straně a pak rovnoběžku správným bodem.

2. Zbylý úhel je 180 - ty zbylé dva. K bodu C postupně přenesu 45 a 30 st. z druhé strany.

Libor, zdravím.

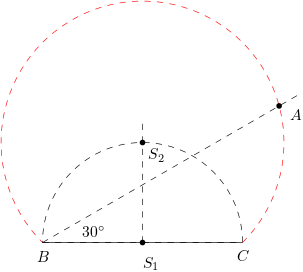
Sestrojíš si úsečku BC. Najdeš její střed \(S_1\) a opíšeš oblouk s poloměrem \(BS_1\). Tím ti vznikne část Thaletovy kružnice, z níž vidíš BC pod úhlem 90°.

Pak ze středu \(S_1\) uděláš kolmici a kde protne ten oblouk, máš bod \(S_2\). Opíšeš oblouk se středem \(S_2\) a poloměrem \(S_2B\) (na obrázku červeně). Na tomto oblouku jsou všechny body, z nichž vidíš BC pod úhlem 45° (jsou to obvodové úhly ke středovému 90°)

Nyní stačí z bodu B narýsovat úhel 30° tak, jak už ti poradili, a máš bod A.

A je hotovo.

Moc děkuji. Je to pro syna, má to za úkol. Moc jste mi pomohli.

Sestrojovat 90°pomocí trojúhelníku s ryskou není ovšem žádná konstrukce, to je pouhé obkreslování úhlu dle fakticky šablony, kdy máme napevno nastavený úhloměr na 90° (to je jako ten trojúhelník s ryskou). Zkonstruovat 45° sice můžeme půlením 90°, jenže nejprve musíme jen s pomocí pravítka, tužky a kružítka vyrobit pravý úhel. To jde snadno, stačí udělat přímku, na ní zvolit bod a udělat kružnici (jakoukoliv a tu samou pak v bodě, kde se protne ta kružnice s přímkou znovu a v průsečíku obou stejných kružnic máme body, které když spojíme, budou protínat původní úsečku pod pravým úhlem. Ten teprve rozpůlíme. Použití umělé pomůcky s pravým úhlem je jinými slovy totéž, jako mít napevno nastavený úhel 30°nebo 45°, prostě není to konstrukce, ale pouhé obkreslování dle již hotové šablony.

Zde v tomto příkladě nejrve uděláme úhel 30° při vrcholu B a pak 105°při vrcholu C. Pro 30°vezmeme do kružítka délku strany a a sestrojíme 60° a ten rozpůlíme. 105°docílíme jako 60°+ 60°- ((60°/2)/2) = 60°+60°- 60°/4 = 60°+ 60°- 15°= 105° a pro kontrolu musí být při vrcholu C úhel 45° při přesném kreslení. Samotných 45°je lépe sestrojit jako 60°-15°, čili jako 60°- 60°/4 (prostě se bude dvakrát půlit), než jako polovina 90°, který sestrojit bez úhloměru (alias trojúhelníku s ryskou) není tak jednoduché.