Výpočet objemu a obsahu pomocí Integrálu

Ahoj Dominiku.

ten první: spočítej si průsečíky těch dvou funkcí a budeš jednoduše integrovat tu větší funkci mínus tu menší. meze budou x1 a x2 průsečíky těch funkcí(resp jejich xové souřadnice) Mám to kdyžtak vysvětlený v kurzu integrálů: https://mathematicator.com/kurz/integraly

Ten druhej se dost blbě popisuje textem. ale nakresli si tu věc, kterou rotuješ. A pak je na to nějakej vzoreček vygoogli si objem rotačního tělesa. Akorát bacha na to, kterej vzoreček použiješ. jedewn je na to když to rotuješ kolem osy x a druhej kolem osy y.

Viz níže : vzorečky nepotřebujete, stačí si umět odvodit diferenciální vztahy

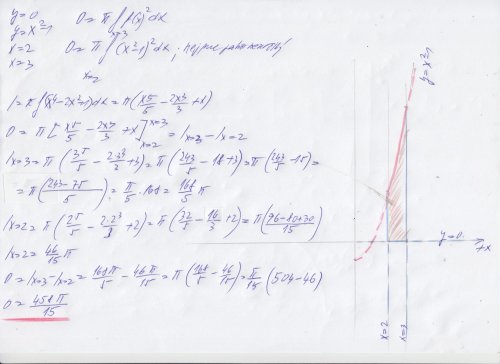
Viz niže, počítáte vlastně zde diferenciání válec, tím poloměrem je f ( x ) horní - f ( x ) dolní , kde dolní je zde = 0, tou výškou je ten diferenciál dx, kteráý narůstá mezi těmi mezemi x dolní, x horní, osou rotace je přímo osa X . Záleží také pochopitelně na poloze osy otáčení, zde to byla přímo osa X, ale může být posunutá, pak se to musí k ní vztahovat tím, že její polohu odečteme.

Kdyby to bylo podle osy Y ta rotace, tak jsou dvě možnosti, buď přeznačit osy a diferencovat funkci x = g ( y ) a tou výškou bude diferenciál dy, ale hraje stejnou roli, jako dx a tím poloměrem diferenciálního válce bude ta funkce x = g ( y ) . Nebo se použije jiný diferenciální vztah, kdy se ale plátkuje tedy po diferenciálních slupkách a ta má nejprve obsah 2 * pi * x * dx a na výšku f ( x ) a to dá pak objem po integraci, prostě se sečte nekonečně mnoho plochých slupek a plochy slupky samotné zase zde vzejdou jako nekonečně mnoho kružnic od nejmenší při středu otáčení až po největší tu hraniční. Zase záleží na ose otáčení, nemusí to být přímo osa Y, ale odsazená rovnoběžně s osou Y, pak by se musila odečítat její poloha (podobně jako u toho diferenciálního válce točeného podle X s odsazenou osou rotace)