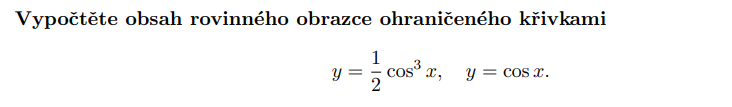Výpočet obsahu rovinného obrazce ohraničeného křivkami

Ten obrazec je periodický a nenulový, tudíž by plocha byla nekonečná. Budeme tedy dále předpokládat, že se bavíme o jednom jeho úseku, a to $x \in \left[ -\frac{ \pi} { 2} ,\frac{ \pi} { 2} \right]$

Počítáme tedy

$\int_{ \frac{ -\pi} { 2} } ^{ \frac{ \pi} { 2} } \cos x - \frac{ 1} { 2} \cos^3 x dx$

Nyní budu upravovat výraz uvnitř integrálu:

$\cos x - \frac{ 1} { 2} \cos^3 x = \frac{ 1} { 2} \cos x \cdot\left(2 - \cos^2 x\right) = \frac{ 1} { 2} \cos x \left( 1 + \sin^2 x\right)$

Nyní provedeme substituci: $y = \sin x$, $dy = \cos x dx$, hranice integrálu budou $[-1,1]$

Celkově tedy

$S = \int_{ -1} ^{ 1} \frac{ 1} { 2} (1+y^2) dy$

S tím už si, předpokládám, poradíš.

Kdyby bylo něco v předchozím postupu nejasné, ptej se.

Děkuji moc, velmi mi to pomohlo a potvrdilo mi to můj postup, ke kterému jsem v průběhu noci došel :-) Jen bych se chtěl zeptat, nemělo by tam být v té závorce:

$1-sin^2(x)$ a nikoliv $1+sin^2(x)$?

Každopádně moc děkuji ! :)

Platí rovnice $\sin^2 x + \cos^2 x = 1$.

Máme tam $2 - \cos^2 x = 1 + (1 - \cos^2 x) = 1 + \sin^2 x$

Jestli jsem dobře vytknul tu polovinu, tak je to v pořádku.

Tak spíše bývá zvykem toto zadávat v 1.kvadrantu, takže asi tam chybí a dále vymezeno přímkami y=0, x=0, což je osa x a y. Pak by to vyšlo pochopitelně poloviční, čili v intervalu <0,pi/2>