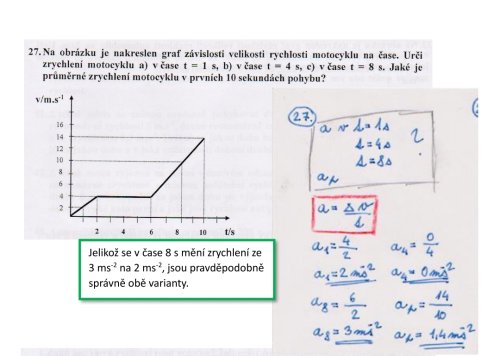
Výpočet zrychlení z grafu

Ahoj Adame,

průměrné zrychlení je dobře, ale vychází mi jinak zrychlení v té třetí části - vezmi si celý ten třetí interval.

Jen poznámky na okraj:

a) má být \( \rm{ m\cdot s^{ -2} } \) s tečkou nebo s mezerou (\( \rm{ m s^{ -2} } \) je "milisekunda na minus druhou")

:-)

b) zrychlení - delta je i ve jmenovateli u času (znamená "přírůstek času"):

\(\displaystyle a=\frac{ \Delta v} { \Delta t} \)

OPRAVA

Nevšiml jsem si, že vodorovná osa není nakreslena přesně "rovnoměrně"...

Jak se píše v rámečku, v čase t = 8 sekud se zrychlení skokově mění ze 3 m/s2 na 2 m/s2. Jaké je zrychlení přesně v okamžiku t = 8 s, to z grafu nemůžeme určit.

Tak nejspíš, je to školometský středoškolský příklad a zrychlení bude buď nulové ( konstantní rychlost ) nebo konstantní ( nenulové ) a pak z toho lineárně narůstající rychlost. Pokud by se to zrychlení měnilo s časem, tak pak je to již ne konstatní zrychlení a = konst, ale a = a ( t ) a to není tak jednoduché s tím pracovat. A co se týče času, tak ten se vždy uvažuje, že plyne konstatně, proto ty grafické intervaly časových úseků musí být stejné ( proto také byl kdysi dohodou zaveden konstantně plynoucí střední sluneční čas v astronomii a tak musí fungovat i časoměry i grafické vyjadřování času ). Takže mezi t = 0 a t= 4 je konstatní zrychlení 2 m / s ^ 2 , mezi t = 2 a t = 6 je zrychlení nulové alias konstantní rychlost, mezi t = 6 a t = 10 je zrychlení konstantní 10 / 4 = 2.5 m / s ^ 2. Více se o tom říci nedá. A tím pádem to platí i pro časy v rámci těch intervalů v t = 1 musí být 2 , v t = 4 musí být 0 v t = 8 musí být 2.5 . Počítat ale prostý aritmetický průměr asi není to pravé, jelikož každý úsek trvá různě, takže spíš vážený obecný průměr , tedy suma delta ti * ai / suma delta t, čili ( 2 * 2 + 4 * 0 + 4 * 2.5 ) / ( 2 + 4 + 4 ) = 1.4 m / s ^ 2

Mně tam teda přijde dost zvláštní ten graf kolem času 8 s. Od 6 do 10 sekund je evidentně lineární, ale přitom podle kótování mezi 6 a 8 s je tam zrychlení \(3 m\cdot s^{ -2} \) a mezi 8 a 10 s je tam zrychlení \(2 m\cdot s^{ -2} \)

Děkuji za Vaše odpovědi, pořád mi ale nejde do hlavy, proč když počítáme zrychlení v čase 1s, proč do vzorce dosazujeme 4/2 když čas má být 1.

Jaká je ta druhá metoda výpočtu průměrného zrychlení? něco jako a=∆v1 + ∆v2 ... / ∆t1 + ∆t2 ... nebo se mýlím a je pouze ta metoda a=14/10?

Předem děkuji

To je přeci jasné, jiné, než konstatní zrychlení Vás neučí, na zrychlení dané obecnou funkcí času nejde použít středoškolský "aparát" potřebuje se na to i dvourozměrný integrál, takže jelikož je konstantní, tak graficky vzato to "a" je u Vás konstanta značená a (ale obecně to je funkce a = a ( t ) ) , tedy u vás konstantní funkce bez ohledu na čas a graficky je to tangenta úhlu té šikmé úsečky, čili ve chvíli, když je rychlost konstantní, tak se zrychlení žádné nekoná alias tg úhlu té úsečky je nula a opravdu, je rovnoběžná s osou času a tam, kde je šikmá, tak je to poměr "svislá" ku "vodorovné, tedy rozdíl rychlostí / rozdíl časů a ten je po celém průběhu té úsečky konstantní. Čili jinými slovy máte tu lineární nárůst rychlosti s ohledem na čas, proto v = a * t, čili "kolik uplyne vteřin, tolik přibyde ( nebo ubyde) rychlosti. Prostě, nemůžete z praktického hlediska dělit nekonečně krátký interval rychlostí nekonečně krátkým intervalem času, to jde v diferenciálním počtu, ale zde to nemá smysl. Ale kdyby ty rychlosti byly dány funkcí času , třeba v = c * tg t, tak ano, v každém okamžiku je jiné zrychlení, jenže pak to nepůjde takto jednoduše, pak se musí derivovat funkce a dosadit do ní právě ten Váš konkrétní časový okamžik abyste dostali zrychlení coby funkci času, tady na času okamžitém v rámci intervalu u toho konstantního zrychlení nezáleží , takže je jedno, jestli zjišťujeme hodnotu konstanty a v čase t = 1, nebo v t = 1.5 pořád bude to na celé té šikmé úsečce konstantní. Kdybyste ale měli např. v = c * tg t, pak třeba v čase t = 1 dostanete a ( t = 1 ) = ( c * 1 / cos ^ 2 t) pro ( t = 1 ) (úhel se musí převést na čas), c je libovolná nenulová počáteční konstanta, třeba = 1 a jiná bude hodnota po dosazení t =1.5 a pak spočíst nějaký průměr také jde, ale již jen pomocí integrálu. Prostě obecně to je i dost složité, tady jednoduché. Jen v tom čase t = 8 to vypadá, že ten Váš učitel zřejmě chtěl nakreslit, že na úsečku o sklonu tg alfa = 3 čili a = 3 navazuje úsečka o menším sklonu tg alfa = 2 čili a = 2 a nevšiml si toho a místo toho dost podivně posunul interval času, ač plyne konstantně. Zřejmě měla být v t = 8 zalomená.

A jinak nejde vůbec přejít skokovitě z "něčeho" na "něco", takže to je jen zidealizovaný případ, ve skutečnosti právě pro přechod z a = 0 na a > 0 nebo z a = 3 na a = 2 je zapotřebí funkce a ( t ) závisící na čase a to se také odehraje na nějakém potřebném časovém intervalu, který zde je uměle = 0, jenže to je nikoliv jednoduché.

Tohle všechno by Vám ale mohli naznačit ti Vaši učitelé a ne držet omertu.

Je otázka, čemu kdo chce říkat průměrná, ale protože jsou různě dlouhé časy, kdy působilo pokaždé jiné zrychlení, tak asi je rozumné vzít v úvahu, že co působí déle by se mělo více uplatnit, než co působí krátší čas, takže to "prostý" aritmetický průměr nebude. (Byl by, pokud by časové intervaly byly stejně dlouhé, pak se ztotožní s tím obecným váženým). Ale obecný vážený, kde "váhy" jsou délky časových intervalů působení konkrétního zrychlení. Nejedná se o tzv. vážený aritmetický průměr, ten je jen jinak přeuspořádaný prostý aritmetický průměr. Čili zde to je suma pi * ai / suma pi, kde za pi zvolíme délky časových intervalů.